题目内容
17.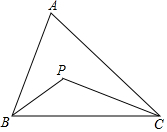 如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )
如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )| A. | 102° | B. | 112° | C. | 115° | D. | 118° |
分析 先根据三角形内角和定理,求得∠ACB度数,再根据角平分线的定义,得出∠PBC=37°,∠PCB=25°,最后根据三角形内角和定理,求得∠P的度数.
解答 解:∵在△ABC中,∠BAC=56°,∠ABC=74°,
∴∠ACB=180°-∠BAC-∠ABC=50°,
∵BP、CP分别平分∠ABC和∠ACB,
∴∠PBC=37°,∠PCB=25°,
∴△BCP中,∠P=180°-∠PBC-∠PCB=118°,
故选:D.
点评 本题主要考查了三角形内角和定理以及角平分线的定义的运用,解题时注意:三角形内角和等于180°.

练习册系列答案
相关题目
7.37058精确到百位的近似数是( )
| A. | 3.71×104 | B. | 3.70×105 | C. | 3.70×104 | D. | 370 |
12.一元二次方程x2-4=0的解是( )
| A. | x=2 | B. | x1=$\sqrt{2}$,x2=-$\sqrt{2}$ | C. | x=-2 | D. | x1=2,x2=-2 |
9. 如图,BC=$\frac{1}{2}$AB,D为AC的中点,若DC=3,则AB的长是( )
如图,BC=$\frac{1}{2}$AB,D为AC的中点,若DC=3,则AB的长是( )
 如图,BC=$\frac{1}{2}$AB,D为AC的中点,若DC=3,则AB的长是( )
如图,BC=$\frac{1}{2}$AB,D为AC的中点,若DC=3,则AB的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
7. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值为( )
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
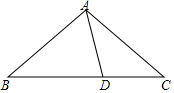 如图,在△ABC中,点D在边BC上,AC=BD,∠CAD=30°,∠ACB=40°,则∠ABC=40°.
如图,在△ABC中,点D在边BC上,AC=BD,∠CAD=30°,∠ACB=40°,则∠ABC=40°.