题目内容
20.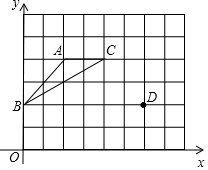 如图,在坐标系的第一象限建立网格,网格中的每个小正方形边长都为1,格点△ABC的顶点坐标分别为A(2,4)、B(0,2)、C(4,4).
如图,在坐标系的第一象限建立网格,网格中的每个小正方形边长都为1,格点△ABC的顶点坐标分别为A(2,4)、B(0,2)、C(4,4).(1)若△ABC外接圆的圆心为P,则点P的坐标为(3,1).
(2)以点D为顶点,在网格中画一个格点△DEF,使△DEF∽△ABC,且相似比为1:2.(画出符合要求的一个三角形即可)
分析 (1)分别作AC、AB的中垂线,两直线的交点即为所求点P;
(2)根据相似比为1:2可得DE=$\sqrt{2}$,DF=1,EF=$\sqrt{5}$,据此可得.
解答 解:(1)如图,
点P即为所求,其坐标为(3,1),
故答案为:(3,1);
(2)如图,△DEF即为所求三角形.
点评 本题主要考查三角形的外心和相似图形,熟练掌握三角形的外心到三顶点的距离相等及相似三角形的性质是解题的关键.

练习册系列答案
相关题目
10.对于二次函数 y=(x-1)2+2 的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 顶点坐标是(-1,2) | C. | 对称轴是x=1 | D. | 与x轴有两个交点 |
15.下列各组数值中,是方程2x-y=8的解的是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0.5}\\{y=-7}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=-2}\end{array}\right.$ |
12.一元二次方程x2-4=0的解是( )
| A. | x=2 | B. | x1=$\sqrt{2}$,x2=-$\sqrt{2}$ | C. | x=-2 | D. | x1=2,x2=-2 |
9. 如图,BC=$\frac{1}{2}$AB,D为AC的中点,若DC=3,则AB的长是( )
如图,BC=$\frac{1}{2}$AB,D为AC的中点,若DC=3,则AB的长是( )
 如图,BC=$\frac{1}{2}$AB,D为AC的中点,若DC=3,则AB的长是( )
如图,BC=$\frac{1}{2}$AB,D为AC的中点,若DC=3,则AB的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
10.某体校的甲、乙两名体育生,在进行10米气手枪设计测试时,每人射击5次,甲体育生射中的环数(单位:环)为:8,6,7,7,7;乙体育生射中的环数(单位:环)为:6,5,9,7,8,则下列说法中不正确的是( )
| A. | 甲体育生此次射击成绩的众数为7环 | |
| B. | 乙体育生此次射击成绩的平均数为7环 | |
| C. | 甲体育生此次射击成绩的成绩比乙体育生的稳定 | |
| D. | 乙体育生此次射击成绩的中位数为6环 |
 如图,已知点A在数轴上对应的数为a,点B对应的数为b,且点O为数轴上的原点,|a+5|+(a+b+1)2=0
如图,已知点A在数轴上对应的数为a,点B对应的数为b,且点O为数轴上的原点,|a+5|+(a+b+1)2=0