题目内容
15．北国超市的小王对该超市苹果的销售进行了统计，某进价为2元/千克的品种的苹果每天的销售量y（千克）和当天的售价x（元/千克）之间满足y=-20x+200（3≤x≤5），若要使该品种苹果当天的利润达到最高，则其售价应为[利润=销售量•（售价-进价）]（ ）| A． | 5元 | B． | 4元 | C． | 3.5元 | D． | 3元 |
分析 设销售这种苹果所获得的利润为w，根据“利润=销售量•（售价-进价）“列出函数解析式，并配方成顶点式，利用二次函数的性质可得其最值情况．
解答 解：设销售这种苹果所获得的利润为w，
则w=（x-2）（-20x+200）
=-20x2+240x-400
=-20（x-6）2+320，
∴当x＜6时，w随x的增大而增大，
∵3≤x≤5，
∴当x=5时，w取得最大值，即该品种苹果当天的利润达到最高，
故选：A．
点评 本题主要考查二次函数的应用，理解题意依据相等关系列出函数解析式配方成顶点式、并熟练掌握二次函数的性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
3．下列从左到右变形正确的是（ ）
| A． | $\frac{0.2a+b}{a+0.2b}=\frac{2a+b}{a+2b}$ | B． | $\frac{{x-\frac{1}{2}y}}{{\frac{1}{2}x+y}}=\frac{2x-y}{x+2y}$ | ||
| C． | $-\frac{x+1}{x-y}=\frac{x-1}{x-y}$ | D． | $\frac{a+b}{a-b}=\frac{a-b}{a+b}$ |
10．某体校的甲、乙两名体育生，在进行10米气手枪设计测试时，每人射击5次，甲体育生射中的环数（单位：环）为：8，6，7，7，7；乙体育生射中的环数（单位：环）为：6，5，9，7，8，则下列说法中不正确的是（ ）
| A． | 甲体育生此次射击成绩的众数为7环 | |
| B． | 乙体育生此次射击成绩的平均数为7环 | |
| C． | 甲体育生此次射击成绩的成绩比乙体育生的稳定 | |
| D． | 乙体育生此次射击成绩的中位数为6环 |
20．在函数y=$\frac{\sqrt{x+3}}{2x}$中，自变量x的取值范围是（ ）
| A． | x≥-3且x≠0 | B． | x≤3且x≠0 | C． | x≠0 | D． | x≥-3 |
7．
如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，则sinB的值为（ ）
如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，则sinB的值为（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
4．
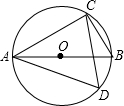如图，已知AB是圆O的直径，∠CAB=30°，则cosD的值为（ ）
如图，已知AB是圆O的直径，∠CAB=30°，则cosD的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\sqrt{3}$ |
5．化简（1-$\frac{2}{x+1}$）÷$\frac{1}{{x}^{2}-1}$的结果是（ ）
| A． | （x+1）2 | B． | （x-1）2 | C． | $\frac{1}{（x+1）^{2}}$ | D． | $\frac{1}{（x-1）^{2}}$ |