题目内容
12.已知方程组$\left\{\begin{array}{l}{x+y=4a+5}\\{x-y=6a-5}\end{array}\right.$的解满足不等式2x-y<6,则a的取值范围是a<1.分析 解方程组得出x、y,将其代入到2x-y<6中可得关于a的不等式,解之即可.
解答 解:解方程组$\left\{\begin{array}{l}{x+y=4a+5}\\{x-y=6a-5}\end{array}\right.$,得:$\left\{\begin{array}{l}{x=5a}\\{y=5-a}\end{array}\right.$,
∵2x-y<6,
∴10a-(5-a)<6,
解得:a<1,
故答案为:a<1.
点评 本题主要考查解二元一次方程组和一元一次不等式的能力,根据题意列出关于a的不等式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.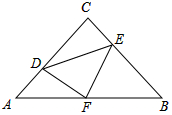 如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动变化过程中,则5个结论:①∠CDF=∠BEF;②△DFE是等腰直角三角形;③四边形CDFE的面积随D,E的运动而变化;④△CDE面积的最大值为4;⑤△DFE面积的最小值为2,其中正确的结论是( )
如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动变化过程中,则5个结论:①∠CDF=∠BEF;②△DFE是等腰直角三角形;③四边形CDFE的面积随D,E的运动而变化;④△CDE面积的最大值为4;⑤△DFE面积的最小值为2,其中正确的结论是( )
 如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动变化过程中,则5个结论:①∠CDF=∠BEF;②△DFE是等腰直角三角形;③四边形CDFE的面积随D,E的运动而变化;④△CDE面积的最大值为4;⑤△DFE面积的最小值为2,其中正确的结论是( )
如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动变化过程中,则5个结论:①∠CDF=∠BEF;②△DFE是等腰直角三角形;③四边形CDFE的面积随D,E的运动而变化;④△CDE面积的最大值为4;⑤△DFE面积的最小值为2,其中正确的结论是( )| A. | ①③⑤ | B. | ②③④ | C. | ①②⑤ | D. | ①②④ |
3.已知a、b是有理数,并且a2=$\frac{4}{9}$,|b|=$\frac{1}{3}$,如果a、b异号,那么a+b的值等于( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | ±1 | D. | ±$\frac{1}{3}$ |
1.菱形的两条对角线长分别是方程x2-14x+48=0的两实根,则菱形的面积为( )
| A. | 48 | B. | 25 | C. | 24 | D. | 12 |
2.若$\sqrt{1-2n}$+$\sqrt{2n-1}$有意义,则(-n)2的平方根是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $±\frac{1}{4}$ | D. | $±\frac{1}{2}$ |
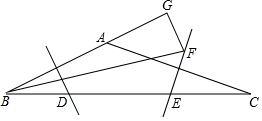 如图,在△ABC中,∠BAC为钝角,边AB、AC的垂直平分线分别交BC于点D、E.
如图,在△ABC中,∠BAC为钝角,边AB、AC的垂直平分线分别交BC于点D、E.
 .
.