题目内容
14．
如图，用三角尺可按下面方法画角平分线：在已知的∠AOB 的两边上分别取点M、N，使OM=ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（ ）| A． | SSS | B． | HL | C． | AAS | D． | SAS |
分析 利用作法可得到OM=ON，PM⊥OM，PN⊥ON，再加上公共边OP，则可利用“HL”判断△POM≌△PON．
解答 解：由作法可得OM=ON，PM⊥OM，PN⊥ON，
则∠PMO=∠PNO=90°，
在Rt△PMO和Rt△PNO中
$\left\{\begin{array}{l}{OP=OP}\\{OM=ON}\end{array}\right.$，
所以△POM≌△PON（HL）．
故选B．
点评 本题考查了基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．也考查了全等三角形的判定方法．
练习册系列答案
优学名师名题系列答案
相关题目
4．
如图，2×5的正方形网格中，用5张1×2的矩形纸片将网格完全覆盖，则不同的覆盖方法有（ ）
如图，2×5的正方形网格中，用5张1×2的矩形纸片将网格完全覆盖，则不同的覆盖方法有（ ）| A． | 3种 | B． | 5种 | C． | 8种 | D． | 13种 |
5．
已知：如图，在直角△ABC中，∠ACB=90°，∠CAB=30°，P为形内一点，∠BPC=120°，若BP=3，则△PAB的面积为（ ）
已知：如图，在直角△ABC中，∠ACB=90°，∠CAB=30°，P为形内一点，∠BPC=120°，若BP=3，则△PAB的面积为（ ）| A． | 9 | B． | 4$\sqrt{3}$ | C． | 3$\sqrt{3}$ | D． | $\frac{9\sqrt{3}}{2}$ |
2．
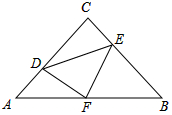如图，在等腰Rt△ABC中，∠C=90°，AC=BC=4，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持AD=CE，连接DE，DF，EF，在此运动变化过程中，则5个结论：①∠CDF=∠BEF；②△DFE是等腰直角三角形；③四边形CDFE的面积随D，E的运动而变化；④△CDE面积的最大值为4；⑤△DFE面积的最小值为2，其中正确的结论是（ ）
如图，在等腰Rt△ABC中，∠C=90°，AC=BC=4，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持AD=CE，连接DE，DF，EF，在此运动变化过程中，则5个结论：①∠CDF=∠BEF；②△DFE是等腰直角三角形；③四边形CDFE的面积随D，E的运动而变化；④△CDE面积的最大值为4；⑤△DFE面积的最小值为2，其中正确的结论是（ ）| A． | ①③⑤ | B． | ②③④ | C． | ①②⑤ | D． | ①②④ |
19．函数y1=k1x+b1与y2=k2x+b2的部分自变量和对应函数值如下：
当y1＞y2时，自变量x的取值范围是（ ）
| x | -4 | -3 | -2 | -1 |
| y | -1 | -2 | -3 | -4 |
| x | -4 | -3 | -2 | -1 |
| y | -9 | -6 | -3 | 0 |
| A． | x＞-2 | B． | x＜-2 | C． | x＞-1 | D． | x＜-1 |
3．已知a、b是有理数，并且a2=$\frac{4}{9}$，|b|=$\frac{1}{3}$，如果a、b异号，那么a+b的值等于（ ）
| A． | 1 | B． | $\frac{1}{3}$ | C． | ±1 | D． | ±$\frac{1}{3}$ |