题目内容
2.计算:(1)($\sqrt{8}$-$\sqrt{27}$)+($\sqrt{48}$-$\sqrt{50}$);
(2)($\sqrt{8}$-2$\sqrt{0.25}$)-($\sqrt{1\frac{1}{8}}$+$\sqrt{50}$+$\frac{2}{3}$$\sqrt{72}$);
(3)($\sqrt{80}$-$\sqrt{1\frac{4}{5}}$)-($\sqrt{3\frac{1}{5}}$+$\frac{4}{5}$$\sqrt{45}$).
分析 (1)先化简二次根式,再去掉括号,合并同类二次根式即可;
(2)先化简二次根式,再去掉括号,合并同类二次根式即可;
(3)先化简二次根式,再去掉括号,合并同类二次根式即可.
解答 解:(1)原式=2$\sqrt{2}$-3$\sqrt{3}$+4$\sqrt{3}$-5$\sqrt{2}$
=$\sqrt{3}$-3$\sqrt{2}$;
(2)原式=2$\sqrt{2}$-$\sqrt{2}$-$\frac{3\sqrt{2}}{4}$-5$\sqrt{2}$-4$\sqrt{2}$
=(2-1-$\frac{3}{4}$-5-4)$\sqrt{2}$
=-$\frac{35\sqrt{2}}{4}$;
(3)原式=4$\sqrt{5}$-$\frac{3\sqrt{5}}{5}$-$\frac{4\sqrt{5}}{5}$-$\frac{12\sqrt{5}}{5}$
=$\frac{\sqrt{5}}{5}$.
点评 本题考查了二次根式的混合运算,把二次根式化为最简二次根式是解题的关键.

练习册系列答案
相关题目
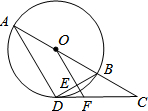 如图,AB是⊙O的直径,C是AB延长线上的一点,CD切⊙O于点D,且∠ABD=2∠BDC.
如图,AB是⊙O的直径,C是AB延长线上的一点,CD切⊙O于点D,且∠ABD=2∠BDC.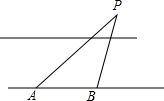 在沿东西走向的河岸南岸,某人自西向东行走,在A处测得河北岸建筑物P在北偏东60°的方向上,某人由A向东走400米到达B处时,在B处测得河北岸物P在北偏东45°的方向上,如果建筑物P距河北岸100米,求河宽.(人与河的距离忽略不计,$\sqrt{3}$≈1.7)
在沿东西走向的河岸南岸,某人自西向东行走,在A处测得河北岸建筑物P在北偏东60°的方向上,某人由A向东走400米到达B处时,在B处测得河北岸物P在北偏东45°的方向上,如果建筑物P距河北岸100米,求河宽.(人与河的距离忽略不计,$\sqrt{3}$≈1.7)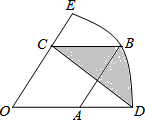 如图,在扇形EOD中,OD=3,菱形OABC的顶点A、B、C分别在OD、$\widehat{DE}$和OE上,OA=$\sqrt{3}$,连接CD,则阴影部分的面积为$\frac{3π-9+3\sqrt{3}}{4}$.
如图,在扇形EOD中,OD=3,菱形OABC的顶点A、B、C分别在OD、$\widehat{DE}$和OE上,OA=$\sqrt{3}$,连接CD,则阴影部分的面积为$\frac{3π-9+3\sqrt{3}}{4}$.