题目内容
14.已知二次函数y=3ax2+2bx-(a+b),当x=0和x=1时,y的值均为正数,则当0<x<1时,抛物线与x轴有2个交点.分析 先利用当x=0和x=1时,y的值均为正数得到-(a+b)>0,3a+2b-(a+b)>0,利用这两个不等式得到a>0,于是判断抛物线开口向上,再计算判别式的值,利用△>0可判断抛物线与x轴有2个交点.
解答 解:∵当x=0和x=1时,y的值均为正数,
∴-(a+b)>0,3a+2b-(a+b)>0,
即a+b<0,2a+b>0,
∴a>0,
∴抛物线开口向上,
∵△=4b2+4•3a(a+b)=(3a+2b)2+3a2,>0,
∴抛物线与x轴有2个交点,
∴当0<x<1时,抛物线与x轴有2个交点.
故答案为2.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
5. 如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( )
如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( )
 如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( )
如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( )| A. | $\frac{5}{2}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | $\frac{7}{4}$ |
 如图所示,AB是⊙O的一条弦,P是⊙O外一点,PB切⊙P于B,PA交⊙O于点C,且AC=BC,PD⊥AB于D,E是AB的中点,求证:PB=2DE.
如图所示,AB是⊙O的一条弦,P是⊙O外一点,PB切⊙P于B,PA交⊙O于点C,且AC=BC,PD⊥AB于D,E是AB的中点,求证:PB=2DE.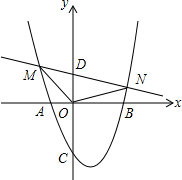 已知,抛物线y=ax2-(a+m-2)x-a-2m+4与x轴交于A(-1,0),B(x,0)两点,与y轴负半轴交于点C,且OA+OB=OC+1.
已知,抛物线y=ax2-(a+m-2)x-a-2m+4与x轴交于A(-1,0),B(x,0)两点,与y轴负半轴交于点C,且OA+OB=OC+1.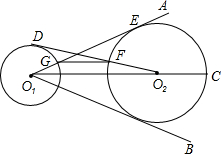 如图,⊙O1与⊙O2外离,O1C是∠AO1B的角平分线,O1C经过点O2,O1A切⊙O2于点E,交⊙O1于点G.
如图,⊙O1与⊙O2外离,O1C是∠AO1B的角平分线,O1C经过点O2,O1A切⊙O2于点E,交⊙O1于点G.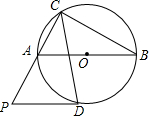 如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的角平分线交⊙O于D,过D作⊙O的切线交CA的延长线于P.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的角平分线交⊙O于D,过D作⊙O的切线交CA的延长线于P.