题目内容
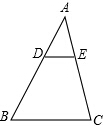如图，在△ABC中，已知DE∥BC，AD=2，AB=6，DE=1.5，求：（1）
| AE |
| AC |
（2）BC的长．
考点：相似三角形的判定与性质
专题：
分析：（1）已知DE∥BC，可证△ADE∽△ABC，利用相似三角形的性质即可求出AE：AC的值；
（2）由（1）可知△ADE∽△ABC，利用相似三角形的性质即可求出BC的长．
（2）由（1）可知△ADE∽△ABC，利用相似三角形的性质即可求出BC的长．
解答：解：（1）∵DE∥BC，
∴△ADE∽△ABC，
∴AD：AB=AE：AC，
∵AD=2，AB=6，
∴AE：AC=1：3；
（2）∵△ADE∽△ABC，
∴DE：BC=AD：AB，
∴1.5：BC=2：6，
∴BC=4.5．
∴△ADE∽△ABC，
∴AD：AB=AE：AC，
∵AD=2，AB=6，
∴AE：AC=1：3；
（2）∵△ADE∽△ABC，
∴DE：BC=AD：AB，
∴1.5：BC=2：6，
∴BC=4.5．
点评：本题考查的是相似三角形的判定与性质，熟知相似三角形对应边的比相等是解答此题的关键．
练习册系列答案
相关题目
如图所示，已知AB∥ED，AB⊥BC，∠BDE=110°，则∠DBC=
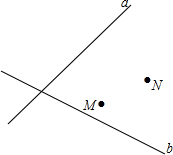（1）a，b分别代表铁路和公路，点M、N分别代表蔬菜和杂货批发市场．现要建中转站O点，使O点到铁路、公路距离相等，且到两市场距离相等．请用尺规画出O点位置，不写作法，保留作图痕迹；
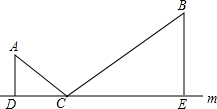如图，AD⊥m，BE⊥m，垂足分别为D，E．AD=1，BE=2，DE=4，点C为直线上的一个动点，则AC+BC的最小值是（ ）
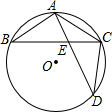如图，在⊙O中，
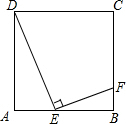如图，E是正方形ABCD的边AB上的动点，EF⊥DE交BC于点F，
如图所示，已知∠AOB和两点M、N，画一点P，使得点P到∠AOB的两边距离相等，