题目内容
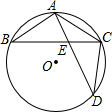 如图,在⊙O中,
如图,在⊙O中, |
| AB |
 |
| AC |
 |
| CD |
考点:相似三角形的判定与性质,圆周角定理,相交弦定理
专题:
分析:由
=
=
,可求得AB=AC,∠CAD=∠B;易证得△CAE∽△CBA,可得AC2=CE•BC=CE2+BE•CE;然后联立由相交弦定理得出的:BE•CE=AD•DE=5;可求得CE的值
 |
| AB |
 |
| AC |
 |
| CD |
解答: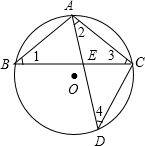 解:∵
解:∵
=
=
,
∴∠1=∠2=∠3=∠4;
∴△AEC∽△BAC;
∴CE:AC=AC:BC;
∵AC=AB=3,因此CE•BC=3×3=9;
∵BC=BE+CE,
∴CE(BE+CE)=9,整理得:CE•BE+CE2=9 ①;
由根据相交弦定理得,BE•CE=AE•ED=5 ②;
②代入①得:5+CE2=9,
解得:CE=2.
 解:∵
解:∵ |
| AB |
 |
| AC |
 |
| CD |
∴∠1=∠2=∠3=∠4;
∴△AEC∽△BAC;
∴CE:AC=AC:BC;
∵AC=AB=3,因此CE•BC=3×3=9;
∵BC=BE+CE,
∴CE(BE+CE)=9,整理得:CE•BE+CE2=9 ①;
由根据相交弦定理得,BE•CE=AE•ED=5 ②;
②代入①得:5+CE2=9,
解得:CE=2.
点评:本题考查了圆周角定理、相似三角形的判定和性质以及相较弦定理的运用,解题的关键是利用相似三角形的性质,建立起各条线段间的关系,结合相交弦定理解答.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
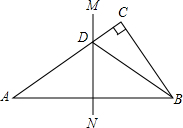 如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若BC=4cm,则BD的长为( )
如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若BC=4cm,则BD的长为( )| A、4cm | B、5cm |
| C、6cm | D、7cm |
下列各组中两项属于同类项的是( )
| A、-x2y和2xy2 |
| B、2x2y与-x2yz |
| C、3m3n和-nm3 |
| D、2n2m与-2m2n |
在0,-9,-|-3|,-(-5),5,6.8中,正整数的个数是( )
| A、1 | B、2 | C、3 | D、4 |
 如图,点C在线段AB上,AB=acm,点MN分别是AC、BC的中点,求线段MN的长.
如图,点C在线段AB上,AB=acm,点MN分别是AC、BC的中点,求线段MN的长.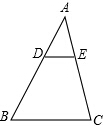 如图,在△ABC中,已知DE∥BC,AD=2,AB=6,DE=1.5,求:
如图,在△ABC中,已知DE∥BC,AD=2,AB=6,DE=1.5,求: 已知△ABC中,DE∥BC,BE,CD相交于F,连结AF并延长交于BC于N.求证:M、N分别是DE、BC的中点吗?
已知△ABC中,DE∥BC,BE,CD相交于F,连结AF并延长交于BC于N.求证:M、N分别是DE、BC的中点吗? 如图,△ABC是边长为8的等边三角形,请你建立适当的平面直角坐标系,并求出A.B.C三个顶点的坐标.
如图,△ABC是边长为8的等边三角形,请你建立适当的平面直角坐标系,并求出A.B.C三个顶点的坐标.