题目内容
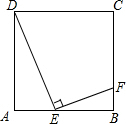 如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F,
如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F,(1)求证:△ADE∽△BEF;
(2)设正方形的边长为8,AE=x,BF=y,请解决下列问题:
①求y与x的函数关系式;
②在AB边上是否存在点E,使得BF=3?若存在,求出x的值;若不存在,请说明理由.
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:(1)证明∠A=∠B,∠ADE=∠BEF,即可解决问题.
(2)证明AD=8,BE=8-x;由△ADE∽△BEF,得到AD:BE=AE:BF,化简、整理即可解决问题.
(3)由题意得到x2-8x+24=0,证明该方程的判别式△<0,即可解决问题.
(2)证明AD=8,BE=8-x;由△ADE∽△BEF,得到AD:BE=AE:BF,化简、整理即可解决问题.
(3)由题意得到x2-8x+24=0,证明该方程的判别式△<0,即可解决问题.
解答: 解:(1)∵四边形ABCD为正方形,
解:(1)∵四边形ABCD为正方形,
∴∠A=∠B=90°;
又∵EF⊥DE,
∴∠ADE+∠AED=∠AED+∠BEF,
∴∠ADE=∠BEF,而∠A=∠B,
∴△ADE∽△BEF.
(2)①∵正方形的边长为8,AE=x,
∴AD=8,BE=8-x;
∵△ADE∽△BEF,
∴AD:BE=AE:BF,
∴BF=-
x2+x,
即y=-
x2+x.
(3)若BF=3,则-
x2+x=3,
即x2-8x+24=0,
∵判别式△=64-4×24<0,
∴该方程无解,
故这样的点E不存在.
 解:(1)∵四边形ABCD为正方形,
解:(1)∵四边形ABCD为正方形,∴∠A=∠B=90°;
又∵EF⊥DE,
∴∠ADE+∠AED=∠AED+∠BEF,
∴∠ADE=∠BEF,而∠A=∠B,
∴△ADE∽△BEF.
(2)①∵正方形的边长为8,AE=x,
∴AD=8,BE=8-x;
∵△ADE∽△BEF,
∴AD:BE=AE:BF,
∴BF=-
| 1 |
| 8 |
即y=-
| 1 |
| 8 |
(3)若BF=3,则-
| 1 |
| 8 |
即x2-8x+24=0,
∵判别式△=64-4×24<0,
∴该方程无解,
故这样的点E不存在.
点评:该题以正方形为载体,以正方形的性质、相似三角形的判定及其性质等为考查的核心构造而成;灵活运用有关定理来解题是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各组中两项属于同类项的是( )
| A、-x2y和2xy2 |
| B、2x2y与-x2yz |
| C、3m3n和-nm3 |
| D、2n2m与-2m2n |
在0,-9,-|-3|,-(-5),5,6.8中,正整数的个数是( )
| A、1 | B、2 | C、3 | D、4 |
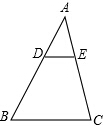 如图,在△ABC中,已知DE∥BC,AD=2,AB=6,DE=1.5,求:
如图,在△ABC中,已知DE∥BC,AD=2,AB=6,DE=1.5,求: 已知△ABC中,DE∥BC,BE,CD相交于F,连结AF并延长交于BC于N.求证:M、N分别是DE、BC的中点吗?
已知△ABC中,DE∥BC,BE,CD相交于F,连结AF并延长交于BC于N.求证:M、N分别是DE、BC的中点吗?