题目内容
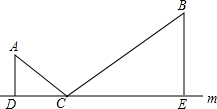 如图,AD⊥m,BE⊥m,垂足分别为D,E.AD=1,BE=2,DE=4,点C为直线上的一个动点,则AC+BC的最小值是( )
如图,AD⊥m,BE⊥m,垂足分别为D,E.AD=1,BE=2,DE=4,点C为直线上的一个动点,则AC+BC的最小值是( )| A、7 | B、5 | C、4.5 | D、4 |
考点:轴对称-最短路线问题
专题:
分析:作出A点关于直线DE的对称点A′,连接A′B,交直线m于点C,则C即为所求点,利用两点间的距离公式即可求解.
解答: 解:如图所示:
解:如图所示:
作出A点关于直线m的对称点A′,连接A′B,交直线m于点C,则C即为所求点,即当三点在一条直线上时有最小值,过A′作A′F⊥BE交BE的延长线于F,
∵AD⊥m,BE⊥m,
∴四边形DEFA′是矩形,
∴AD=A′D=1,BF=2+1=3,A′F=DE=4,
即AC+BC=A′B=
=5.
故选B.
 解:如图所示:
解:如图所示:作出A点关于直线m的对称点A′,连接A′B,交直线m于点C,则C即为所求点,即当三点在一条直线上时有最小值,过A′作A′F⊥BE交BE的延长线于F,
∵AD⊥m,BE⊥m,
∴四边形DEFA′是矩形,
∴AD=A′D=1,BF=2+1=3,A′F=DE=4,
即AC+BC=A′B=
| 32+42 |
故选B.
点评:本题考查的是最短线路问题及两点间的距离公式,解答此题的关键是熟知两点之间线段最短的知识.

练习册系列答案
相关题目
下列四个式子中,计算结果最小的是( )
| A、(-2)2 |
| B、(-3)×22 |
| C、-42÷(-2) |
| D、-32-1 |
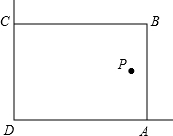 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm. 
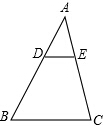 如图,在△ABC中,已知DE∥BC,AD=2,AB=6,DE=1.5,求:
如图,在△ABC中,已知DE∥BC,AD=2,AB=6,DE=1.5,求: 已知△ABC中,DE∥BC,BE,CD相交于F,连结AF并延长交于BC于N.求证:M、N分别是DE、BC的中点吗?
已知△ABC中,DE∥BC,BE,CD相交于F,连结AF并延长交于BC于N.求证:M、N分别是DE、BC的中点吗? 如图:
如图: