题目内容
3.网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,消费者在网店购买某种商品后,对其有“好评”、“中评”、“差评”三种评价,假设这三种评价是等可能的.
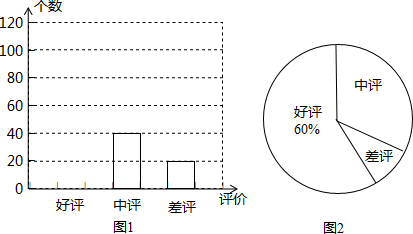
(1)小明对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图.
利用图中所提供的信息解决以下问题:
①小明一共统计了150个评价;
②请将图1补充完整;
③图2中“差评”所占的百分比是13.3%;
(2)若甲、乙两名消费者在该网店购买了同一商品,请你用列表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率.
分析 (1)①用“中评”、“差评”的人数除以二者的百分比之和可得总人数;②用总人数减去“中评”、“差评”的人数可得“好评”的人数,补全条形图即可;③根据$\frac{“差评”人数}{总人数}$×100%可得;
(2)可通过列表表示出甲、乙对商品评价的所有可能结果数,通过概率公式计算可得.
解答 解:(1)①小明统计的评价一共有:$\frac{40+20}{1-60%}$=150(个);
②“好评”一共有150×60%=90(个),补全条形图如图1:
③图2中“差评”所占的百分比是:$\frac{20}{150}$×100%=13.3%;
(2)列表如下:
| 好 | 中 | 差 | |
| 好 | 好,好 | 好,中 | 好,差 |
| 中 | 中,好 | 中,中 | 中,差 |
| 差 | 差,好 | 差,中 | 差,差 |
∴两人中至少有一个给“好评”的概率是$\frac{5}{9}$.
故答案为:(1)①150;③13.3%.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
13.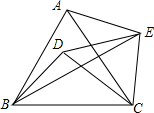 如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
 如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
11.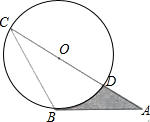 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )
 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{\sqrt{3}}{2}$-$\frac{π}{6}$ | D. | $\frac{\sqrt{3}}{3}$-$\frac{π}{6}$ |
18. 如图,⊙O的半径为1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是( )
如图,⊙O的半径为1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是( )
 如图,⊙O的半径为1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是( )
如图,⊙O的半径为1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是( )| A. |  | B. | 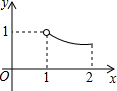 | C. |  | D. |  |
8. 如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
 如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )| A. | 75°36′ | B. | 75°12′ | C. | 74°36′ | D. | 74°12′ |
15.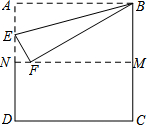 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
12.已知x1、x2是一元二次方程3x2=6-2x的两根,则x1-x1x2+x2的值是( )
| A. | $-\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $-\frac{8}{3}$ | D. | $\frac{4}{3}$ |
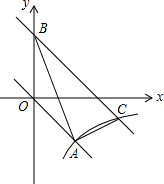 如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).
如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).