题目内容
15.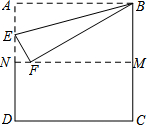 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
分析 根据翻折不变性,AB=FB=2,BM=1,在Rt△BFM中,可利用勾股定理求出FM的值.
解答 解:∵四边形ABCD为正方形,AB=2,过点B折叠纸片,使点A落在MN上的点F处,
∴FB=AB=2,BM=1,
则在Rt△BMF中,
FM=$\sqrt{B{F}^{2}-B{M}^{2}}=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$,
故选:B.
点评 此题考查了翻折变换的性质,适时利用勾股定理是解答此类问题的关键.

练习册系列答案
相关题目
7.$-\frac{1}{2016}$的倒数的绝对值是( )
| A. | -2016 | B. | $\frac{1}{2016}$ | C. | 2016 | D. | $-\frac{1}{2016}$ |
4.若分式$\frac{x-1}{x+2}$的值为0,则( )
| A. | x=-2 | B. | x=0 | C. | x=1 | D. | x=1或-2 |
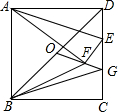 如图,在正方形ABCD中,AB=6,点E在边CD上,DE=$\frac{1}{3}$DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是$\frac{12}{5}$($\sqrt{5}$+$\sqrt{10}$).
如图,在正方形ABCD中,AB=6,点E在边CD上,DE=$\frac{1}{3}$DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是$\frac{12}{5}$($\sqrt{5}$+$\sqrt{10}$). 已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.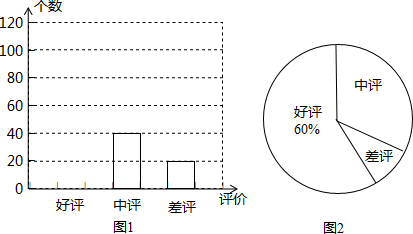
 有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )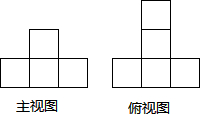 用若干个大小相同的小正方形体组合成的几何体的主视图和俯视图如图所示,下面所给的四个选项中,不可能是这个几何体的左视图的是( )
用若干个大小相同的小正方形体组合成的几何体的主视图和俯视图如图所示,下面所给的四个选项中,不可能是这个几何体的左视图的是( )


 如图,⊙O1与⊙O2相交于A、B两点,过A点的直线与过B点的直线分别交两圆于C、D和E、F,求证:CE∥DF.
如图,⊙O1与⊙O2相交于A、B两点,过A点的直线与过B点的直线分别交两圆于C、D和E、F,求证:CE∥DF.