题目内容
18. 如图,⊙O的半径为1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是( )
如图,⊙O的半径为1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是( )| A. |  | B. | 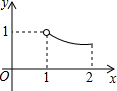 | C. |  | D. |  |
分析 根据题意分1<x≤$\sqrt{2}$与$\sqrt{2}$<x≤2两种情况,确定出y与x的关系式,即可确定出图象.
解答 解:当P在OC上运动时,根据题意得:sin∠APB=$\frac{OA}{AP}$,
∵OA=1,AP=x,sin∠APB=y,
∴xy=1,即y=$\frac{1}{x}$(1<x≤$\sqrt{2}$),
当P在$\widehat{CD}$上运动时,∠APB=$\frac{1}{2}$∠AOB=45°,
此时y=$\frac{\sqrt{2}}{2}$($\sqrt{2}$<x≤2),
图象为:
故选C.
点评 此题考查了动点问题的函数图象,列出y与x的函数关系式是解本题的关键.

练习册系列答案
相关题目
9.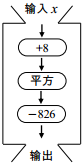 输入一组数据,按下列程序进行计算,输出结果如表:
输入一组数据,按下列程序进行计算,输出结果如表:
分析表格中的数据,估计方程(x+8)2-826=0的一个正数解x的大致范围为( )
 输入一组数据,按下列程序进行计算,输出结果如表:
输入一组数据,按下列程序进行计算,输出结果如表:| x | 20.5 | 20.6 | 20.7 | 20.8 | 20.9 |
| 输出 | -13.75 | -8.04 | -2.31 | 3.44 | 9.21 |
| A. | 20.5<x<20.6 | B. | 20.6<x<20.7 | C. | 20.7<x<20.8 | D. | 20.8<x<20.9 |
7.$-\frac{1}{2016}$的倒数的绝对值是( )
| A. | -2016 | B. | $\frac{1}{2016}$ | C. | 2016 | D. | $-\frac{1}{2016}$ |
 已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.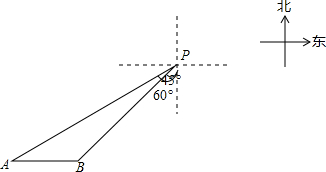 一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?
一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?
 有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )