题目内容
11.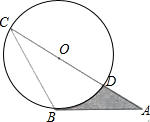 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{\sqrt{3}}{2}$-$\frac{π}{6}$ | D. | $\frac{\sqrt{3}}{3}$-$\frac{π}{6}$ |
分析 首先求出∠AOB,OB,然后利用S阴=S△ABO-S扇形OBD计算即可.
解答 解:连接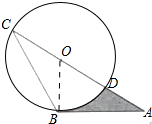 OB.
OB.
∵AB是⊙O切线,
∴OB⊥AB,
∵OC=OB,∠C=30°,
∴∠C=∠OBC=30°,
∴∠AOB=∠C+∠OBC=60°,
在RT△ABO中,∵∠ABO=90°,AB=$\sqrt{3}$,∠A=30°,
∴OB=1,
∴S阴=S△ABO-S扇形OBD=$\frac{1}{2}$×1×$\sqrt{3}$-$\frac{60π•{1}^{2}}{360}$=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
故选C.
点评 本题考查切线的性质、等腰三角形的性质、勾股定理,直角三角形30度角性质,解题的关键是学会分割法求面积,记住扇形面积公式,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.从-1,0,π,3中随机任取一数,取到无理数的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
2.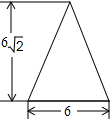 如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
 如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )| A. | 90° | B. | 120° | C. | 135° | D. | 150° |
1.据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为( )
| A. | 3.386×108 | B. | 0.3386×109 | C. | 33.86×107 | D. | 3.386×109 |
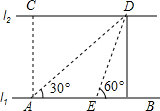 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离. 已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2. 如图,是我们数学课本上采用的科学计算器面板,利用该型号计算器计算$\sqrt{2}$cos55°,按键顺序正确的是( )
如图,是我们数学课本上采用的科学计算器面板,利用该型号计算器计算$\sqrt{2}$cos55°,按键顺序正确的是( )



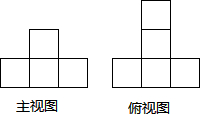 用若干个大小相同的小正方形体组合成的几何体的主视图和俯视图如图所示,下面所给的四个选项中,不可能是这个几何体的左视图的是( )
用若干个大小相同的小正方形体组合成的几何体的主视图和俯视图如图所示,下面所给的四个选项中,不可能是这个几何体的左视图的是( )