题目内容
14.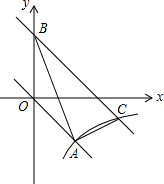 如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).
如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于点B,与反比例函数图象在第四象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积.
分析 (1)将点A坐标(2,-2)分别代入y=kx、y=$\frac{m}{x}$求得k、m的值即可;
(2)由题意得平移后直线解析式,即可知点B坐标,联立方程组求解可得第四象限内的交点C得坐标,可将△ABC的面积转化为△OBC的面积.
解答 解:(1)根据题意,将点A(2,-2)代入y=kx,得:-2=2k,
解得:k=-1,
∴正比例函数的解析式为:y=-x,
将点A(2,-2)代入y=$\frac{m}{x}$,得:-2=$\frac{m}{2}$,
解得:m=-4;
∴反比例函数的解析式为:y=-$\frac{4}{x}$;
(2)直线OA:y=-x向上平移3个单位后解析式为:y=-x+3,
则点B的坐标为(0,3),
联立两函数解析式$\left\{\begin{array}{l}{y=-x+3}\\{y=-\frac{4}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$,
∴第四象限内的交点C的坐标为(4,-1),
∵OA∥BC,
∴S△ABC=S△OBC=$\frac{1}{2}$×BO×xC=$\frac{1}{2}$×3×4=6.
点评 此题考查了反比例函数与一次函数的交点问题,涉及的知识有:坐标与图形性质,直线与坐标轴的交点,待定系数法求函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
4.已知二次函数y=x2-2x-3,点P在该函数的图象上,点P到x轴、y轴的距离分别为d1、d2.设d=d1+d2,下列结论中:
①d没有最大值;
②d没有最小值;
③-1<x<3时,d随x的增大而增大;
④满足d=5的点P有四个.
其中正确结论的个数有( )
①d没有最大值;
②d没有最小值;
③-1<x<3时,d随x的增大而增大;
④满足d=5的点P有四个.
其中正确结论的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.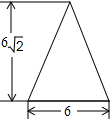 如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
 如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )| A. | 90° | B. | 120° | C. | 135° | D. | 150° |
9.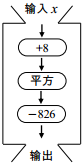 输入一组数据,按下列程序进行计算,输出结果如表:
输入一组数据,按下列程序进行计算,输出结果如表:
分析表格中的数据,估计方程(x+8)2-826=0的一个正数解x的大致范围为( )
 输入一组数据,按下列程序进行计算,输出结果如表:
输入一组数据,按下列程序进行计算,输出结果如表:| x | 20.5 | 20.6 | 20.7 | 20.8 | 20.9 |
| 输出 | -13.75 | -8.04 | -2.31 | 3.44 | 9.21 |
| A. | 20.5<x<20.6 | B. | 20.6<x<20.7 | C. | 20.7<x<20.8 | D. | 20.8<x<20.9 |
4.若分式$\frac{x-1}{x+2}$的值为0,则( )
| A. | x=-2 | B. | x=0 | C. | x=1 | D. | x=1或-2 |
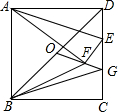 如图,在正方形ABCD中,AB=6,点E在边CD上,DE=$\frac{1}{3}$DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是$\frac{12}{5}$($\sqrt{5}$+$\sqrt{10}$).
如图,在正方形ABCD中,AB=6,点E在边CD上,DE=$\frac{1}{3}$DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是$\frac{12}{5}$($\sqrt{5}$+$\sqrt{10}$).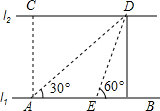 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离. 已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.