题目内容
13.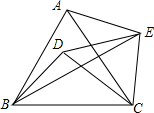 如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 首先由△ABC和△EDC都是正三角形,易证得△BCD≌△ACE,然后由全等三角形的对应角相等,求得∠BDC+∠DEB=∠AEB+60°,又由在△DBE中,∠BDE+∠DEB+∠DBE=180°,即可求得答案.
解答 解:∴CD=CE,∠DCE=60°,
∴△EDC是等边三角形
∵△ABC是等边三角形,
∴BC=AC,DC=EC,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{DC=EC}\end{array}\right.$,
∴△BCD≌△ACE(SAS),
∴∠BDC=∠AEC=∠AEB+∠CED-∠DEB=∠AEB+60°-∠DEB,
∴∠BDC+∠DEB=∠AEB+60°,
∵在△DBE中,∠BDE+∠DEB+∠DBE=180°,
即∠BDC+∠CDE+∠DEB+∠DBE=180°,
∴∠DBE=180°-(∠BDC+∠CDE+∠DEB)=180°-45°-60°-60°=15°
故选:A.
点评 此题考查了全等三角形的判定与性质.解决本题的关键是证明△BCD≌△ACE,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.已知二次函数y=x2-2x-3,点P在该函数的图象上,点P到x轴、y轴的距离分别为d1、d2.设d=d1+d2,下列结论中:
①d没有最大值;
②d没有最小值;
③-1<x<3时,d随x的增大而增大;
④满足d=5的点P有四个.
其中正确结论的个数有( )
①d没有最大值;
②d没有最小值;
③-1<x<3时,d随x的增大而增大;
④满足d=5的点P有四个.
其中正确结论的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.从-1,0,π,3中随机任取一数,取到无理数的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
18.某校对全体学生开展心理健康知识测试,七、八、九三个年级共有800名学生,各年级的合格人数如表所示,则下列说法正确的是( )
| 年级 | 七年级 | 八年级 | 九年级 |
| 合格人数 | 270 | 262 | 254 |
| A. | 七年级的合格率最高 | B. | 八年级的学生人数为262名 | ||
| C. | 八年级的合格率高于全校的合格率 | D. | 九年级的合格人数最少 |
2.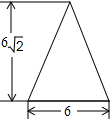 如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
 如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )| A. | 90° | B. | 120° | C. | 135° | D. | 150° |
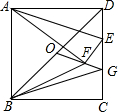 如图,在正方形ABCD中,AB=6,点E在边CD上,DE=$\frac{1}{3}$DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是$\frac{12}{5}$($\sqrt{5}$+$\sqrt{10}$).
如图,在正方形ABCD中,AB=6,点E在边CD上,DE=$\frac{1}{3}$DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是$\frac{12}{5}$($\sqrt{5}$+$\sqrt{10}$).