题目内容
如图,在□ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB= _________cm.
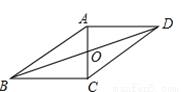
 【解析】试题解析:∵四边形ABCD是平行四边形,
故答案为: .
【解析】试题解析:∵四边形ABCD是平行四边形,
故答案为: .
练习册系列答案
相关题目
解下列分式方程.
(1) 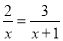 ; (2)
; (2) 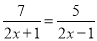 ;
;
(3) 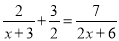 ; (4)
; (4) 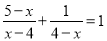 .
.
 (1) x=2.(2) x=3.(3) x=-2. (4)无解.
【解析】试题分析:每个方程确定最简公分母后,方程两边乘最简公分母,把分式方程转化为整式方程求解后再进行检验即可得.
试题解析:(1)方程两边同乘x(x+1),得
2(x+1)=3x,
解得:x=2,
检验:当x=2时,x(x+1)≠0,
所以原方程的解为x=2;
(2)方程两边同乘(2x-1...
(1) x=2.(2) x=3.(3) x=-2. (4)无解.
【解析】试题分析:每个方程确定最简公分母后,方程两边乘最简公分母,把分式方程转化为整式方程求解后再进行检验即可得.
试题解析:(1)方程两边同乘x(x+1),得
2(x+1)=3x,
解得:x=2,
检验:当x=2时,x(x+1)≠0,
所以原方程的解为x=2;
(2)方程两边同乘(2x-1... 一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为_________小时(用根号表示).
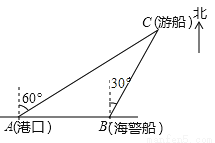
 【解析】试题分析:过点C作CD⊥AB,则在Rt△ACD中,AC=60海里,∠CAD=30°可得:CD=30海里;在Rt△CBD中,∠CBD=60°,则BC=20海里,则t=20÷40=小时.
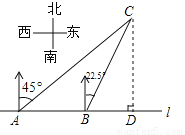
【解析】试题分析:过点C作CD⊥AB,则在Rt△ACD中,AC=60海里,∠CAD=30°可得:CD=30海里;在Rt△CBD中,∠CBD=60°,则BC=20海里,则t=20÷40=小时. 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A. 4km B. (2+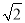 )km C. 2
)km C. 2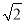 km D. (4-
km D. (4-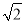 )km
)km
 B
【解析】试题分析:根据题意中方位角的特点,过点B作BE⊥AC,交AC于点E,由∠CAB=45°,AB=2km,可知BE=km,根据题意还可知∠BCA=∠BCD=22.5°,因此CB是∠ACD的角平分线,根据角平分线的性质可得:BD=BE=km,因此CD=AD=AB+BD=(2+)km,故选B.
B
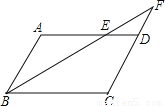
【解析】试题分析:根据题意中方位角的特点,过点B作BE⊥AC,交AC于点E,由∠CAB=45°,AB=2km,可知BE=km,根据题意还可知∠BCA=∠BCD=22.5°,因此CB是∠ACD的角平分线,根据角平分线的性质可得:BD=BE=km,因此CD=AD=AB+BD=(2+)km,故选B. 如图,在平行四边形ABCD中,若AB=6,AD=10,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
 4
【解析】
试题分析:首先根据平行四边形的性质可得AB=DC=6,AD=BC=10,AB∥DC,再根据平行线的性质与角平分线的性质证明∠2=∠3,根据等角对等边可得BC=CF=10,再用CF﹣CD即可算出DF的长.
试题解析:∵四边形ABCD为平行四边形,∴AB=DC=6,AD=BC=10,AB∥DC. ∵AB∥DC,∴∠1=∠3,
又∵BF平分∠ABC,∴∠1=∠2,∴...
4
【解析】
试题分析:首先根据平行四边形的性质可得AB=DC=6,AD=BC=10,AB∥DC,再根据平行线的性质与角平分线的性质证明∠2=∠3,根据等角对等边可得BC=CF=10,再用CF﹣CD即可算出DF的长.
试题解析:∵四边形ABCD为平行四边形,∴AB=DC=6,AD=BC=10,AB∥DC. ∵AB∥DC,∴∠1=∠3,
又∵BF平分∠ABC,∴∠1=∠2,∴... 如图,等腰梯形ABCD下底与上底的差恰好等于腰长,DE∥AB.则∠DEC等于( )
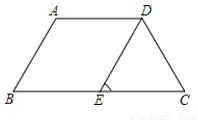
A. 75° B. 60° C. 45° D. 30°
 B
【解析】试题解析:∵DE∥AB,AD∥BC,
∴四边形ABED为平行四边形,
∴AD=BE,
∵BC-AD=AB=EC,
∵等腰梯形ABCD,
∴AB=DC=EC,
∴为等边三角形,
∴∠DEC=60°.
故选B.
B
【解析】试题解析:∵DE∥AB,AD∥BC,
∴四边形ABED为平行四边形,
∴AD=BE,
∵BC-AD=AB=EC,
∵等腰梯形ABCD,
∴AB=DC=EC,
∴为等边三角形,
∴∠DEC=60°.
故选B. 如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )
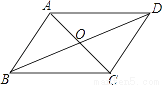
A. AO=OD B. AO⊥OD C. AO=OC D. AO⊥AB
 C
【解析】试题分析:对角线不一定相等,A错误;
对角线不一定互相垂直,B错误;
对角线互相平分,C正确;
对角线与边不一定垂直,D错误.
故选C.
C
【解析】试题分析:对角线不一定相等,A错误;
对角线不一定互相垂直,B错误;
对角线互相平分,C正确;
对角线与边不一定垂直,D错误.
故选C. 在多边形的内角中,锐角的个数不能多于( )
A. 2个 B. 3个 C. 4个 D. 5个
 B
【解析】多边形的外角和是360°,因此外角中最多有三个钝角,外角与相邻的内角互为邻补角,
所以在多边形的内角中,锐角的个数不能多于3个,
故选B.
B
【解析】多边形的外角和是360°,因此外角中最多有三个钝角,外角与相邻的内角互为邻补角,
所以在多边形的内角中,锐角的个数不能多于3个,
故选B. 若对于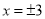 以外的一切数
以外的一切数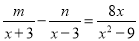 均成立,则
均成立,则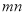 的值是( )
的值是( )
A. 8 B. 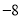 C. 16 D.
C. 16 D. 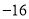
 D
【解析】,则 ,得: .
故选D.
D
【解析】,则 ,得: .
故选D. 
