题目内容
如图，等腰梯形ABCD下底与上底的差恰好等于腰长，DE∥AB．则∠DEC等于（ ）
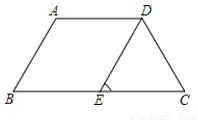
A. 75° B. 60° C. 45° D. 30°
B
【解析】试题解析：∵DE∥AB，AD∥BC,
∴四边形ABED为平行四边形,
∴AD=BE,
∵BC-AD=AB=EC,
∵等腰梯形ABCD,
∴AB=DC=EC,
∴为等边三角形,
∴∠DEC=60°.
故选B．
练习册系列答案
相关题目
当a＝_______时，方程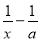
＝2的解为4．
【解析】由题意得： ，
解得：a=，
经检验a=符合原方程，
故答案为： . 如图，甲、乙两船同时从港口O出发，其中甲船沿北偏西30°方向航行，乙船沿南偏西70°方向航行，已知两船的航行速度相同，如果1小时后甲、乙两船分别到达点A、B处，那么点B位于点A的（ ）
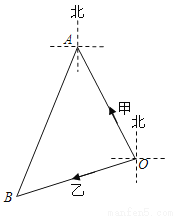
A. 南偏西40° B. 南偏西30° C. 南偏西20° D. 南偏西10°
C
【解析】试题分析：由甲船沿北偏西30°方向航行，乙船沿南偏西70°方向航行，得出∠BOA的度数，由两船的航行速度相同，得出AO=BO，得出∠BAO=50°，以及求出∠BAD的度数，得出点B位于点A的方向，故本题选C． 如图，在□ABCD中，AC交BD于点O，点E、点F分别是OA、OC的中点，请判断线段BE、DF的关系，并证明你的结论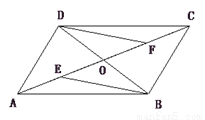
【解析】根据平行四边形的性质对角线互相平分得出OA=OC，OB=OD，利用中点的意义得出OE=OF，从而利用平行四边形的判定定理“对角线互相平分的四边形是平行四边形”判定BFDE是平行四边形，从而得出BE=DF，BE∥DF．
【解析】
由题意得：BE=DF，BE∥DF．理由如下：
连接DE、BF．
∵ABCD是平行四边形，
∴OA=OC，OB=OD，
∵E，F分别是... 如图，在□ABCD中，AC，BD相交于点O，AB=10cm，AD=8cm，AC⊥BC，则OB= _________cm．
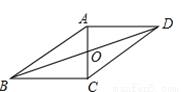
【解析】试题解析：∵四边形ABCD是平行四边形，
故答案为: ． 平行四边形的对角线一定具有的性质是（ ）
A. 相等 B. 互相平分
C. 互相垂直 D. 互相垂直且相等
B
【解析】试题分析：根据平行四边形的对角线互相平分可得答案．
【解析】
平行四边形的对角线互相平分，
故选：B． 在四边形ABCD中,如果∠A:∠B:∠C:∠D=1:2:3:4,则∠D=______
144°
【解析】设∠A=x°，则∠B=2x°，∠C=3x°，∠D=4x°，
∵∠A+∠B+∠C+∠D=360°，
∴x+2x+3x+4x=360，
解得x=36°，
∴2x=72°，3x=108°，4x=144°，
所以∠A=36°，∠B=72°，∠C=108°，∠D=144°，
故答案为：144°. 某学生在计算四个多边形的内角和时，得到下列四个答案，其中错误的是（ ）
A. 180° B. 540° C. 1900° D. 1080°
C
【解析】多边形的内角和公式是(n-2)•180°，内角和是180°时候是三角形；内角和是540°时候是五边形；内角和是1080°的时候是十边形，内角和是1900°时候算出来的边数不是整数，所以错误的是C，
故选C. 先化简，再求值．
(1) 
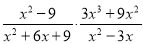，其中x＝-
．
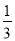（2）
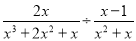，其中x=－2．
（3）
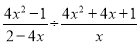，其中x=-
．
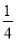（4）若1＜x＜2，化简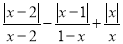
．
⑴－１，⑵ ，⑶，⑷1．
【解析】试题分析：（1）原式约分得到最简结果，将x的值代入计算即可求出值；
（2）原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算，约分得到最简结果，将x的值代入计算即可求出值；
（3）原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算，约分得到最简结果，将x的值代入计算即可求出值．
（4）根据绝对值的化简原则进行化简，进行运算即可....