题目内容
在多边形的内角中,锐角的个数不能多于( )
A. 2个 B. 3个 C. 4个 D. 5个
 B
【解析】多边形的外角和是360°,因此外角中最多有三个钝角,外角与相邻的内角互为邻补角,
所以在多边形的内角中,锐角的个数不能多于3个,
故选B.
B
【解析】多边形的外角和是360°,因此外角中最多有三个钝角,外角与相邻的内角互为邻补角,
所以在多边形的内角中,锐角的个数不能多于3个,
故选B.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知二次函数的图象开口向上,且顶点在y轴的负半轴上,请你写出一个满足条件的二次函数的表达式________.
 y=x2-2
【解析】依题意,只要满足二次项系数为正数,顶点坐标为(0,k),k<0即可,
根据顶点式写解析式,本题答案不唯一,如y=x²-2.故答案为:y=x2-2.
y=x2-2
【解析】依题意,只要满足二次项系数为正数,顶点坐标为(0,k),k<0即可,
根据顶点式写解析式,本题答案不唯一,如y=x²-2.故答案为:y=x2-2. 如图,在□ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB= _________cm.
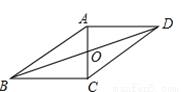
 【解析】试题解析:∵四边形ABCD是平行四边形,
故答案为: .
【解析】试题解析:∵四边形ABCD是平行四边形,
故答案为: . 在四边形ABCD中,如果∠A:∠B:∠C:∠D=1:2:3:4,则∠D=______
 144°
【解析】设∠A=x°,则∠B=2x°,∠C=3x°,∠D=4x°,
∵∠A+∠B+∠C+∠D=360°,
∴x+2x+3x+4x=360,
解得x=36°,
∴2x=72°,3x=108°,4x=144°,
所以∠A=36°,∠B=72°,∠C=108°,∠D=144°,
故答案为:144°.
144°
【解析】设∠A=x°,则∠B=2x°,∠C=3x°,∠D=4x°,
∵∠A+∠B+∠C+∠D=360°,
∴x+2x+3x+4x=360,
解得x=36°,
∴2x=72°,3x=108°,4x=144°,
所以∠A=36°,∠B=72°,∠C=108°,∠D=144°,
故答案为:144°. 若一个多边形的边数增加1,则它的内角和增加 __________________
 180°
【解析】设多边形边数为n,那么增加1条即为n+1,
原来内角和:(n-2)×180°=n×180°-360°,
现在内角和:(n+1-2)×180°=n×180°-180°,
内角和增加了180°,
故答案为:180°.
180°
【解析】设多边形边数为n,那么增加1条即为n+1,
原来内角和:(n-2)×180°=n×180°-360°,
现在内角和:(n+1-2)×180°=n×180°-180°,
内角和增加了180°,
故答案为:180°. 某学生在计算四个多边形的内角和时,得到下列四个答案,其中错误的是( )
A. 180° B. 540° C. 1900° D. 1080°
 C
【解析】多边形的内角和公式是(n-2)•180°,内角和是180°时候是三角形;内角和是540°时候是五边形;内角和是1080°的时候是十边形,内角和是1900°时候算出来的边数不是整数,所以错误的是C,
故选C.
C
【解析】多边形的内角和公式是(n-2)•180°,内角和是180°时候是三角形;内角和是540°时候是五边形;内角和是1080°的时候是十边形,内角和是1900°时候算出来的边数不是整数,所以错误的是C,
故选C. 解分式方程:
(1)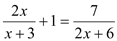
(2)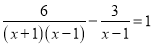
 (1) (2)x=-4
【解析】【试题分析】(1)方程两边同时乘以 ,则 ;移项及合并得: 系数化为1: .经检验: 是原方程的根.
(2)方程两边同时乘以 ,去分母得: 去括号得: 移项得: 解得: 经检验,x=-4是原方程的根.
【试题解析】
方程两边同时乘以 ,则 ;
移项及合并得:
系数化为1: .
经检验: 是原方程的根.
方程两边同时乘以...
(1) (2)x=-4
【解析】【试题分析】(1)方程两边同时乘以 ,则 ;移项及合并得: 系数化为1: .经检验: 是原方程的根.
(2)方程两边同时乘以 ,去分母得: 去括号得: 移项得: 解得: 经检验,x=-4是原方程的根.
【试题解析】
方程两边同时乘以 ,则 ;
移项及合并得:
系数化为1: .
经检验: 是原方程的根.
方程两边同时乘以... 若分式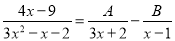 (A、B为常数),则A、B 的值为 ( )
(A、B为常数),则A、B 的值为 ( )
A. 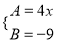 B.
B. 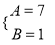 C.
C. 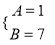 D.
D. 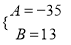
 B
【解析】= ,则 ,故选B.
B
【解析】= ,则 ,故选B. 当y=x+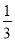 时,
时,  的值是_________.
的值是_________.
 -3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3.
-3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3. 
