题目内容
19. 如图,∠AOB=60°,其内部的点M到OA的距离MF=1,到OB的距离ME=2,求线段OM的长.
如图,∠AOB=60°,其内部的点M到OA的距离MF=1,到OB的距离ME=2,求线段OM的长.
分析 延长EM交OA于H,应用30°角所对的直角边等于斜边的一半求出MH,再根据特殊角的三角函数值求出OE,最后根据勾股定理可以求出OM的长.
解答 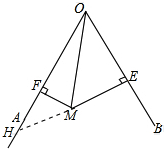 解:延长EM交OA于H,
解:延长EM交OA于H,
∵∠AOB=60°,
∴∠OHE=30°,
在Rt△HMF中,
∵∠OHE=30°,
∴MH=2MF=2,
∴EH=EM+MH=2+2=4,
∴tan∠OHE=tan30°=$\frac{OE}{HE}$=$\frac{OE}{4}$,
∴OE=$\frac{4\sqrt{3}}{3}$,
在Rt△OEM中,OM=$\sqrt{O{E}^{2}+M{E}^{2}}$=$\sqrt{(\frac{4\sqrt{3}}{3})^{2}+{2}^{2}}$=$\frac{2\sqrt{21}}{3}$.
点评 此题考查了勾股定理、特殊角的三角函数值和在直角三角形中,30°所对的直角边等于斜边的一半,关键是根据题意作出辅助线,构造直角三角形.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | 三个角对应相等的两个三角形全等 | |
| B. | 两个三角形全等,则对应边上的高对应相等 | |
| C. | 周长和一个角对应相等的两个三角形全等 | |
| D. | 两个三角形全等,面积不一定相等 |
 如图,在△ABC中,点D、E、F分别在BC、AB、AC上.BD=CF,BE=CD,DG⊥EF于点G,且EG=FG.求证:AB=AC.
如图,在△ABC中,点D、E、F分别在BC、AB、AC上.BD=CF,BE=CD,DG⊥EF于点G,且EG=FG.求证:AB=AC. 已知△ABC为等边三角形,延长BC到M,CA到N,使CM=AN,连BN交MA的延长线于Q,求∠BQM.
已知△ABC为等边三角形,延长BC到M,CA到N,使CM=AN,连BN交MA的延长线于Q,求∠BQM. 如图,已知AC⊥BD于点E,AB=BC,求证:∠1=∠2.
如图,已知AC⊥BD于点E,AB=BC,求证:∠1=∠2.