题目内容
10. 如图,在△ABC中,点D、E、F分别在BC、AB、AC上.BD=CF,BE=CD,DG⊥EF于点G,且EG=FG.求证:AB=AC.
如图,在△ABC中,点D、E、F分别在BC、AB、AC上.BD=CF,BE=CD,DG⊥EF于点G,且EG=FG.求证:AB=AC.
分析 连接DE、DF,由线段垂直平分线的性质得出DE=DF,由SSS证得△BDE≌△CFD,得出∠B=∠C,即可得出结论.
解答 证明:连接DE、DF,如图所示:
∵DG⊥EF于点G,且EG=FG,
∴DE=DF,
在△BDE和△CFD中,
$\left\{\begin{array}{l}{BD=CF}\\{BE=CD}\\{DE=DF}\end{array}\right.$,
∴△BDE≌△CFD(SSS),
∴∠B=∠C,
∴AB=AC.
点评 本题考查了全等三角形的判定与性质、线段垂直平分线的性质、等腰三角形的判定;熟练掌握线段垂直平分线的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
18.如图1,在四边形ABCD中,∠D=60°,点P,Q同时从点D出发,以每秒1个单位长度的速度分别沿D→A→B→C和D→C→B方向运动至相遇时停止,连接PQ.设点P运动的路程为x,PQ的长y,y与x之间满足的函数关系的图象如图2,则下列说法中不正确的是( )

| A. | AB∥CD | B. | AB=8 | ||
| C. | S四边形ABCD=$\frac{161\sqrt{3}}{4}$ | D. | ∠B=135° |
20.为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房建设力度.2013年市政府共投资2亿元人民币建设廉租房8万平方米,预计到2015年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率都为x,可列方程( )
| A. | 2x2=9.5 | B. | 2+2(x+1)+2(x+1)2=9.5 | ||
| C. | 2(x+1)2=9.5 | D. | 2+2(x+1)+(x+1)2=9.5×8 |
 如右图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长.
如右图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长.
 如图,在四边形ABCD中,AB=CD,AD=BC,试判断AB与CD是否平行,并说明理由.
如图,在四边形ABCD中,AB=CD,AD=BC,试判断AB与CD是否平行,并说明理由.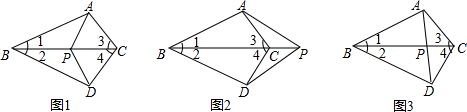
 如图,在△ABC中,AB=AC,BD=CD,则∠B=∠C,请说明理由.
如图,在△ABC中,AB=AC,BD=CD,则∠B=∠C,请说明理由. 如图,∠AOB=60°,其内部的点M到OA的距离MF=1,到OB的距离ME=2,求线段OM的长.
如图,∠AOB=60°,其内部的点M到OA的距离MF=1,到OB的距离ME=2,求线段OM的长.