题目内容
2. 如图,四边形ABCD是菱形,E在AD上,F在AB延长线上,CE和DF相交于点G,若CE=DF,∠CGF=30°,AB的长为6,则菱形ABCD的面积为18.
如图,四边形ABCD是菱形,E在AD上,F在AB延长线上,CE和DF相交于点G,若CE=DF,∠CGF=30°,AB的长为6,则菱形ABCD的面积为18.
分析 作辅助线,构建全等三角形,根据中位线定理得OM=$\frac{1}{2}$CE,ON=$\frac{1}{2}$DF,则OM=ON,证明△AMO≌△AHO,得OM=OH=ON,根据等边对等角和平角的定义得:∠AMO+∠ONH=180,再由平行线的同位角相等得:∠DAB+∠EGF=180°,所以得∠DAB=30°,根据30°角的性质求出菱形的高PC的长,代入面积公式求出菱形ABCD的面积.
解答 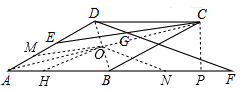 解:连接AC、BD,交于点O,分别取AE、BF的中点M、N,连接OM、ON,在AB上截取AH=AM,连接OH,过C作CP⊥AF于P,
解:连接AC、BD,交于点O,分别取AE、BF的中点M、N,连接OM、ON,在AB上截取AH=AM,连接OH,过C作CP⊥AF于P,
∵四边形ABCD是菱形,
∴O是BD的中点,也是AC的中点,
∴OM=$\frac{1}{2}$CE,ON=$\frac{1}{2}$DF,
∵CE=DF,
∴OM=ON,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∵AO=AO,
∴△AMO≌△AHO,
∴OM=OH,∠AMO=∠AHO,
∴OM=OH=ON,
∴∠OHN=∠ONH,
∵∠AHO+∠OHN=180°,
∴∠AMO+∠ONH=180,
∵OM∥EC,ON∥DF,
∴∠AMO=∠AEC,∠ONH=∠GFA,
∴∠AEC+∠GFA=180°,
∴∠DAB+∠EGF=180°,
∵∠CGF=30°,
∴∠EGF=150°,
∴∠DAB=30°,
∵AD∥BC,
∴∠CBF=∠DAB=30°,
∵AB=BC=6,
∴CP=$\frac{1}{2}$BC=3,
∴菱形ABCD的面积=AB•CP=6×3=18,
故答案为18.
点评 本题考查了菱形的性质,还考查了全等三角形、中位线、等腰三角形的性质和判定,取中点连线段,构建中位线定理与已知线段相结合,再利用三角形全等,求出∠DAB=30°,从而使问题得以解决.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
13.某商品价格a元,降低15%后又降价10%,销售额猛增,商店决定再提价20%,提价后这种产品价格为( )
| A. | a元 | B. | 0.918a元 | C. | 0.972a元 | D. | 0.96a元 |
10.在一次游戏晚会上,老师出了一道题让小明猜一个自然数,题目如下:甲:这个数是9;乙:这个数是质数;丙:这个数是偶数;丁:这个数是15.若甲和乙之中有一个对,丙和丁之中有一个对,则这个数是( )
| A. | 3 | B. | 5 | C. | 2 | D. | 6 |
7.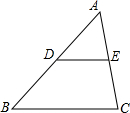 如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )
如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )
 如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )
如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )| A. | BC=2DE | B. | △ADE∽△ABC | C. | $\frac{AD}{AE}$=$\frac{AB}{AC}$ | D. | S△ABC=2S△ADE |
14.下列各对数中,互为同类项的是( )
| A. | 3x2y和-2xy2 | B. | πxy和-2xy2 | C. | 7xy3和y3x | D. | 3mn和2m2n |
12.比-6大2的数是( )
| A. | -8 | B. | -4 | C. | 4 | D. | 8 |
