题目内容
6．
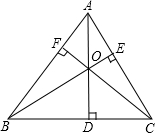如图，△ABC的三条高AD、BE、CF相交于点O．（1）在△BOC中，OB边上的高是CE，OC边上的高是BF，BC边上的高是OD．
（2）在△AOC中，OA边上的高是CD，OC边上的高是AF，AC边上的高是OE．
（3）在△AOB中，OA边上的高是BD，OB边上的高是AE，AB边上的高是OF．
分析 从三角形的一个顶点向底边作垂线，垂足与顶点之间的线段叫做三角形的高，根据三角形高的定义判断．
解答 解：（1）由图可得，在△BOC中，OB边上的高是CE，OC边上的高是BF，BC边上的高是OD．（2）由图可得，在△AOC中，OA边上的高是CD，OC边上的高是AF，AC边上的高是OE．
（3）由图可得，在△AOB中，OA边上的高是BD，OB边上的高是AE，AB边上的高是OF．
故答案为：CE，BF，OD；CD，AF，OE；BD，AE，OF．
点评 本题主要考查了三角形高线的定义，解决问题的关键是掌握：钝角三角形有两条高在三角形外部，一条高在三角形内部，三条高所在直线相交于三角形外一点．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
14．
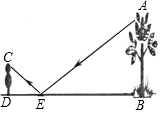如图，王华把一面很小的镜子水平放置在离树底（点B）8米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢（点A），已知DE=4米，王华目高CD=1.6米，则树的高度AB为（ ）
如图，王华把一面很小的镜子水平放置在离树底（点B）8米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢（点A），已知DE=4米，王华目高CD=1.6米，则树的高度AB为（ ）| A． | 4.8米 | B． | 3.2米 | C． | 8米 | D． | 20米 |
18．
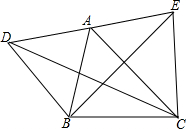如图，A为DE的中点，设S1=S△DBC，S2=S△ABC，S3=S△EBC，则S1，S2，S3的关系是（ ）
如图，A为DE的中点，设S1=S△DBC，S2=S△ABC，S3=S△EBC，则S1，S2，S3的关系是（ ）| A． | S2=$\frac{3}{2}$（S1+S3） | B． | S2=$\frac{1}{2}$（S3-S1） | C． | S2=$\frac{1}{2}$（S1+S3） | D． | S2=$\frac{3}{2}$（S3-S1） |