题目内容
18.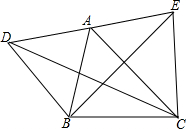 如图,A为DE的中点,设S1=S△DBC,S2=S△ABC,S3=S△EBC,则S1,S2,S3的关系是( )
如图,A为DE的中点,设S1=S△DBC,S2=S△ABC,S3=S△EBC,则S1,S2,S3的关系是( )| A. | S2=$\frac{3}{2}$(S1+S3) | B. | S2=$\frac{1}{2}$(S3-S1) | C. | S2=$\frac{1}{2}$(S1+S3) | D. | S2=$\frac{3}{2}$(S3-S1) |
分析 作DM⊥BC于M,AN⊥BC于N,EH⊥BC于H,根据梯形中位线定理得到AN=$\frac{1}{2}$(DM+EH),根据三角形的面积公式计算即可判断.
解答 解: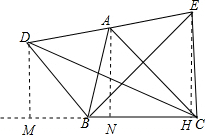 作DM⊥BC于M,AN⊥BC于N,EH⊥BC于H,
作DM⊥BC于M,AN⊥BC于N,EH⊥BC于H,
则DM∥AN∥EH,
∵A为DE的中点,
∴AN是梯形DMHE的中位线,
∴AN=$\frac{1}{2}$(DM+EH),
S1+S3=$\frac{1}{2}$×BC×DM+$\frac{1}{2}$×BC×EH=$\frac{1}{2}$×BC×(DM+EH)=$\frac{1}{2}$×BC×2AN=2S2,
∴S2=$\frac{1}{2}$(S1+S3),
故选:C.
点评 本题考查的是三角形的面积计算,掌握三角形的面积公式、梯形的中位线定理是解题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
13.在四边形ABCD中,若$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,且|$\overrightarrow{AB}$|=|$\overrightarrow{AD}$|,则四边形ABCD为( )
| A. | 矩形 | B. | 菱形 | ||
| C. | 正方形 | D. | 不是矩形、菱形的四边形 |
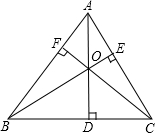 如图,△ABC的三条高AD、BE、CF相交于点O.
如图,△ABC的三条高AD、BE、CF相交于点O.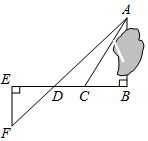 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上,有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A、B间距离的有( )
为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上,有四位同学分别测量出以下四组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A、B间距离的有( )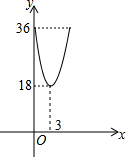 已知两个正方形的面积和y与其中一个正方形边长x之间的函数解析式y=ax2-12x+36的图象如图所示,(3,18)是该图象的顶点,当x=4时,这两个正方形的面积和为( )
已知两个正方形的面积和y与其中一个正方形边长x之间的函数解析式y=ax2-12x+36的图象如图所示,(3,18)是该图象的顶点,当x=4时,这两个正方形的面积和为( )