题目内容
16.若[m]表示不大于m的最大整数,例如:[5]=5,[-3,6]=-4,则关于x的方程[$\frac{3x+1}{7}$-5]=7的整数解有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据题目中[m]的定义把方程转化为一个关于x的不等式组,求得x 范围,然后确定x的整数解即可.
解答 解:根据题意得$\left\{\begin{array}{l}{\frac{3x+1}{7}-5≥7}\\{\frac{3x+1}{7}-5<8}\end{array}\right.$,
解①得x≥$\frac{83}{3}$,
解②得x<30.
则不等式组的解集是$\frac{83}{3}$≤x<30.
则整数解有28,29.
故选B.
点评 本题考查了不等式组的解法,正确理解[m]的定义,转化为一个关于x的不等式组是关键.

练习册系列答案
相关题目
7.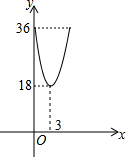 已知两个正方形的面积和y与其中一个正方形边长x之间的函数解析式y=ax2-12x+36的图象如图所示,(3,18)是该图象的顶点,当x=4时,这两个正方形的面积和为( )
已知两个正方形的面积和y与其中一个正方形边长x之间的函数解析式y=ax2-12x+36的图象如图所示,(3,18)是该图象的顶点,当x=4时,这两个正方形的面积和为( )
 已知两个正方形的面积和y与其中一个正方形边长x之间的函数解析式y=ax2-12x+36的图象如图所示,(3,18)是该图象的顶点,当x=4时,这两个正方形的面积和为( )
已知两个正方形的面积和y与其中一个正方形边长x之间的函数解析式y=ax2-12x+36的图象如图所示,(3,18)是该图象的顶点,当x=4时,这两个正方形的面积和为( )| A. | 19 | B. | 20 | C. | 22 | D. | 24 |
4.适合|2a+5|+|2a-3|=8的整数a的值有( )
| A. | 4个 | B. | 5个 | C. | 7个 | D. | 9个 |
5.下列各点不在反比例函数y=$\frac{12}{x}$上的是( )
| A. | (3,4) | B. | (-3,-4) | C. | (6,-2) | D. | (-6,-2) |
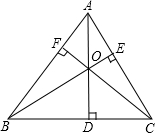 如图,△ABC的三条高AD、BE、CF相交于点O.
如图,△ABC的三条高AD、BE、CF相交于点O.