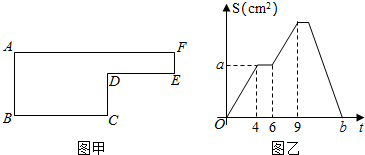
题目内容
10．小明在梳理平行四边形、矩形、菱形、正方形的性质时，发现它们的对角线都具有一个共同的性质，这条性质是对角线（ ）| A． | 互相平分 | B． | 相等 | C． | 互相垂直 | D． | 平分一组对角 |
分析 根据平行四边形、正方形、矩形的性质可知，它们的对角线都具有同一性质是：对角线互相平分．
解答 解：因为矩形、菱形、正方形都是特殊的平行四边形，而平行四边形的对角线互相平分，
所以平行四边形、矩形、菱形、正方形的对角线都具有一个共同的性质，这条性质是对角线互相平分．
故选A．
点评 此题综合考查了平行四边形、矩形、菱形、正方形的对角线的性质．用到的知识点：平行四边形的对角线互相平分；矩形的对角线相等且互相平分；菱形的两条对角线互相垂直平分，并且每一条对角线平分一组对角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角．
练习册系列答案
相关题目
已知直线a∥b，一块直角三角板如图所示放置，若∠1=37°，则∠2=53°．
如图，一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A，B两点，且与x轴交于点C，点A的坐标为（2，1）．
5．某电视机厂一月份生产a台电视机，二、三月份连续增产，每次增长率相同为x，该厂第一季度的产量比一月份翻两番，列方程正确的是（ ）
| A． | a（1+x）2=2a | B． | a+a（1+x）+a（1+x）2=2a | C． | a+a（1+x）+a（1+x）2=4a | D． | a（1+x）2=4a |
15．已知α、β均为锐角，且满足|sinα-$\frac{1}{2}$|+$\sqrt{（tanβ-1）^{2}}$=0，则α+β=（ ）
| A． | 60° | B． | 75° | C． | 90° | D． | 105° |
2．
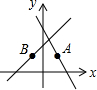如图，在平面直角坐标系中，点A（1，m）在直线y=-2x+3上，点A关于y轴的对称点恰好落在直线y=kx+2上，则k的值为（ ）
如图，在平面直角坐标系中，点A（1，m）在直线y=-2x+3上，点A关于y轴的对称点恰好落在直线y=kx+2上，则k的值为（ ）| A． | -2 | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
