题目内容
20.已知动点P以每秒2cm的速度沿图甲的边框按B⇒C⇒D⇒E⇒F⇒A的路径移动,相应的三角形ABP的面积S(cm2)与时间t(秒)之间的关系用图乙中的图象表示,若AB=6cm,试回答下列问题:(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
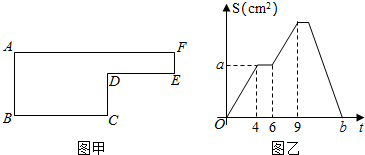
分析 (1)根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度,可得BC的长;
(2)由(1)可得BC的长,又由AB=6cm,可以计算出△ABP的面积,计算可得a的值.
解答 解:(1)动点P在BC上运动时,对应的时间为0到4秒,易得:BC=2cm/秒×4秒=8cm;
故图甲中的BC长是8cm.
(2)由(1)可得,BC=8cm,则:a=$\frac{1}{2}$×BC×AB=24cm2;
图乙中的a是24cm2.
点评 本题考查动点问题的函数图象,解题的关键是读懂图意,明确横轴与纵轴的意义.

练习册系列答案
相关题目
10.小明在梳理平行四边形、矩形、菱形、正方形的性质时,发现它们的对角线都具有一个共同的性质,这条性质是对角线( )
| A. | 互相平分 | B. | 相等 | C. | 互相垂直 | D. | 平分一组对角 |
11. 如图,点A,B,C是直线l上的三个点,若AC=15,BC=2AB,则AB的长是( )
如图,点A,B,C是直线l上的三个点,若AC=15,BC=2AB,则AB的长是( )
 如图,点A,B,C是直线l上的三个点,若AC=15,BC=2AB,则AB的长是( )
如图,点A,B,C是直线l上的三个点,若AC=15,BC=2AB,则AB的长是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
5.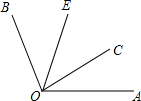 如图,已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠BOE=40°时,∠AOB的度数是( )
如图,已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠BOE=40°时,∠AOB的度数是( )
 如图,已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠BOE=40°时,∠AOB的度数是( )
如图,已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠BOE=40°时,∠AOB的度数是( )| A. | 70° | B. | 80° | C. | 100° | D. | 110° |
10.一条开口向下的抛物线的顶点坐标是(2,3),则这条抛物线有( )
| A. | 最大值3 | B. | 最小值3 | C. | 最大值2 | D. | 最小值-2 |
 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°,BD=3,CE=2,则△ABC的边长为9.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°,BD=3,CE=2,则△ABC的边长为9.