题目内容
4．三个连续偶数的和是24，设中间的偶数为n，则可列出的方程为（ ）| A． | n+（n+2）+（n+4）=24 | B． | n+（n-2）+（n-4）=24 | C． | （n-2）+n+（n+2）=24 | D． | （n-4）+2n+（n+4）=24 |
分析 设中间的偶数为n，则其他的两个为n-2，n+2，根据三个连续偶数的和是24列出方程即可．
解答 解：设中间的偶数为n，则其他的两个为n-2，n+2，根据题意得
（n-2）+n+（n+2）=24．
故选：C．
点评 此题主要考查了由实际问题抽象出一元一次方程，根据题意，理解相邻两个偶数之间的差，正确利用等量关系列出方程．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
15．下列叙述正确的是（ ）
| A． | 两个有理数相加，和一定比每个加数都大 | |
| B． | 两个有理数相加，只需把绝对值相加 | |
| C． | 两个有理数相加，和非正即负 | |
| D． | 两个有理数相加，必须确定和的符号和绝对值 |
如图，在△ABC中，三个内角的角平分线交于点O，OF⊥BC于点E，若∠AOB=130°，求∠COF的度数．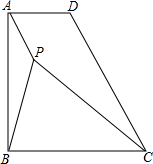
已知在直角梯形ABCD中，∠ABC=90°，AB=BC，点P是梯形内一点，且PA=1，PB=2，PC=3
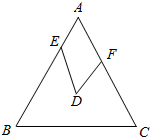如图，已知点D是边长为1的等边三角形ABC的内心，点E，F分别在边AB，AC上，且满足∠EDF=60°，求△AEF的周长．
如图，小正方形网格边长均为1，△ABC顶点都在格点上，请你判断△ABC的形状是等腰直角三角形，请说明理由．
实数a，b在数轴上对应的位置如图示：