题目内容
14. 实数a,b在数轴上对应的位置如图示:
实数a,b在数轴上对应的位置如图示:则$\root{3}{{{{(a+b)}^3}}}+|\sqrt{{{(a-b)}^2}}$-b|=b.
分析 根据图示知a<0<b,|a|>|b|,依此化简$\root{3}{{{{(a+b)}^3}}}+|\sqrt{{{(a-b)}^2}}$-b|即可.
解答 解:根据图示知a<0<b,|a|>|b|,
则$\root{3}{{{{(a+b)}^3}}}+|\sqrt{{{(a-b)}^2}}$-b|
=a+b+||a-b|-b|
=a+b+|-a+b-b|
=a+b-a
=b.
故答案为:b.
点评 本题考查了实数与数轴的对应关系、三次根式的性质与化简、二次根式的性质与化简.解答此类题目时应先根据由数轴上a,b两点的位置确定a,b的符号及绝对值的大小,然后再根据三次根式和二次根式的性质解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.三个连续偶数的和是24,设中间的偶数为n,则可列出的方程为( )
| A. | n+(n+2)+(n+4)=24 | B. | n+(n-2)+(n-4)=24 | C. | (n-2)+n+(n+2)=24 | D. | (n-4)+2n+(n+4)=24 |
9.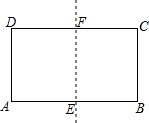 将矩形ABCD沿两条较长边的中点对折得到矩形ADFE,若矩形ADFE∽矩形ABCD,且AB=4,则AD的长等于( )
将矩形ABCD沿两条较长边的中点对折得到矩形ADFE,若矩形ADFE∽矩形ABCD,且AB=4,则AD的长等于( )
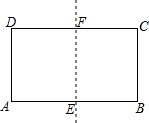 将矩形ABCD沿两条较长边的中点对折得到矩形ADFE,若矩形ADFE∽矩形ABCD,且AB=4,则AD的长等于( )
将矩形ABCD沿两条较长边的中点对折得到矩形ADFE,若矩形ADFE∽矩形ABCD,且AB=4,则AD的长等于( )| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
3.$\sqrt{4}$-1的值是( )
| A. | -1 | B. | 1 | C. | 3 | D. | -3 |
 如图,点D,E在△ABC的边BC上,则图中共有三角形6个.
如图,点D,E在△ABC的边BC上,则图中共有三角形6个.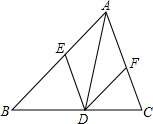 如图,AD是△ABC的一条角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,当∠BAC=90°时,四边形AEDF是正方形.
如图,AD是△ABC的一条角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,当∠BAC=90°时,四边形AEDF是正方形.