题目内容
15. 如图,在△ABC中,三个内角的角平分线交于点O,OF⊥BC于点E,若∠AOB=130°,求∠COF的度数.
如图,在△ABC中,三个内角的角平分线交于点O,OF⊥BC于点E,若∠AOB=130°,求∠COF的度数.
分析 在△AOB中,∠AOB=130°,得到∠ABO+∠BAO=180°-∠AOB=180°-130°=50°,根据AO,BO分别平分∠ABC,∠BAC,得到∠ABC=2∠ABO,∠BAC=2∠BAO,
求得∠ABC+∠BAC=2(∠ABO+∠BAO)=2×50°=100°,所以∠ACB=180°-(∠ABC+∠ACB)=180°-100°=80°,由CO平分∠ACB,所以∠BCO=$\frac{1}{2}$∠ACB=40°,根据OF⊥BC,得到∠COF=90°-∠BCO=90°-40°=50°.
解答 解:∵在△AOB中,∠AOB=130°,
∴∠ABO+∠BAO=180°-∠AOB=180°-130°=50°,
∵AO,BO分别平分∠ABC,∠BAC,
∴∠ABC=2∠ABO,∠BAC=2∠BAO,
∴∠ABC+∠BAC=2(∠ABO+∠BAO)=2×50°=100°,
∴∠ACB=180°-(∠ABC+∠ACB)=180°-100°=80°,
∵CO平分∠ACB,
∴∠BCO=$\frac{1}{2}$∠ACB=40°,
∵OF⊥BC,
∴∠COF=90°-∠BCO=90°-40°=50°.
点评 本题考查了三角形的内角和与角平分线的性质,解决本题的关键是熟记三角形的内角和为180°.

练习册系列答案
相关题目
6.如图,有12个方格,每个方格内有一个数,若相邻三个数的和都是20,则x的位置填的数为15
| -5 | a | b | c | d | e | f | x | g | h | j | 10 |
4.三个连续偶数的和是24,设中间的偶数为n,则可列出的方程为( )
| A. | n+(n+2)+(n+4)=24 | B. | n+(n-2)+(n-4)=24 | C. | (n-2)+n+(n+2)=24 | D. | (n-4)+2n+(n+4)=24 |
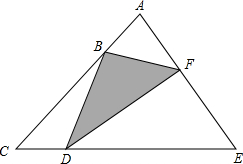 已知S△BDF=19cm2,AB:AC=1:4;AF:AE=1:3;CD:CE=1:5,求△ACE的大小.
已知S△BDF=19cm2,AB:AC=1:4;AF:AE=1:3;CD:CE=1:5,求△ACE的大小.