题目内容
14. 如图,在△ABC中,AC⊥BC,CE⊥AB于E,AF平分∠CAB交CE于点F,过点F作FD∥BC交AB于点D,说明AC=AD成立的理由.
如图,在△ABC中,AC⊥BC,CE⊥AB于E,AF平分∠CAB交CE于点F,过点F作FD∥BC交AB于点D,说明AC=AD成立的理由.
分析 由平行的性质和直角三角形的性质可证明∠ADF=∠B=∠ACF,结合角平分线的定义可证明△ACF≌△ADF,可证得AC=AD.
解答 证明:
∵FD∥BC,
∴∠ADF=∠B,
∵AC⊥BC,CE⊥AB,
∴∠ACB=∠CEB=90°,
∴∠ACF+∠ECB=∠ECB+∠B=90°,
∴∠ACF=∠B,
∴∠ACF=∠ADF,
∵AF平分∠CAB,
∴∠CAF=∠DAF,
在△ACF和△ADF中
$\left\{\begin{array}{l}{∠CAF=∠DAF}\\{∠ACF=∠ADF}\\{AF=AF}\end{array}\right.$
∴△ACF≌△ADF(AAS),
∴AC=AD.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
2.若关于x的一元二次方程ax2-4x+1=0有实数根,则a满足( )
| A. | a≠0 | B. | a≤4 | C. | a≤4且a≠0 | D. | a<4且a≠0 |
9.已知方程x2+nx-1=0的两实数根分别为α、β,则$\frac{β}{α}$+$\frac{α}{β}$的值为( )
| A. | n2+2 | B. | -n2+2 | C. | n2-2 | D. | -n2-2 |
19.某商场购进了一批单价为5元的日用商品,如果以单价7元销售,每天可售出160件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量每天就相应减少20件,设这种商品的销售单价为x元,商场每天销售这种商品y件
(1)给定x的一些值,请计算y的值,填在表中
(2)求y与x之间的函数关系式;
(3)当商品的销售单价定为多少元时,该商品销售这种商品能获得的利润为420元?这时每天销售的商品是多少件?
(1)给定x的一些值,请计算y的值,填在表中
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … | 160 | 140 | 120 | 100 | 80 | … |
(3)当商品的销售单价定为多少元时,该商品销售这种商品能获得的利润为420元?这时每天销售的商品是多少件?
3.已知关于x的方程$\frac{1}{4}$x2-(m-2)x+m2=0有两个相等的实数根,则方程的根为( )
| A. | x1=x2=1 | B. | x1=x2=-2 | C. | x1=x2=-1 | D. | x1=x2=2 |
4.为了打造区域中心城市,实现城市跨越发展,我市新区建设正按投资计划有序进行.新区建设工程部,因道路建设需要开挖土石方,计划每小时挖土石方540m3,现决定向某大型机械租赁公司租甲、乙两种型号的挖掘机来完成这些工作,租赁公司提供的挖掘机有关信息如表:
若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
| 挖掘土石方量(单位:m/台时) | |
| 甲型挖掘机 | 60 |
| 乙型挖掘机 | 80 |
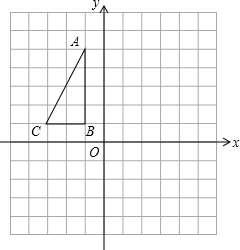 如图,在平面直角坐标系中,ABC的顶点的坐标分别为A(-1,5)、B(-1,1)、C(-3,1).将△ABC向右平移2个单位、再向下平移4个单位得到△A1B1C1;将△ABC绕原点O旋转180°得到△A2B2C2
如图,在平面直角坐标系中,ABC的顶点的坐标分别为A(-1,5)、B(-1,1)、C(-3,1).将△ABC向右平移2个单位、再向下平移4个单位得到△A1B1C1;将△ABC绕原点O旋转180°得到△A2B2C2 某洗衣机洗涤衣服时,经历了进水,清洗,排水脱水四个连续的过程,其中进水,清洗,排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图折线图所示,已知清洗时间为11分钟,排水时间为2分钟,则排水结束时洗衣机中剩下的水量为$\frac{82}{3}$升.
某洗衣机洗涤衣服时,经历了进水,清洗,排水脱水四个连续的过程,其中进水,清洗,排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图折线图所示,已知清洗时间为11分钟,排水时间为2分钟,则排水结束时洗衣机中剩下的水量为$\frac{82}{3}$升.