题目内容
19.某商场购进了一批单价为5元的日用商品,如果以单价7元销售,每天可售出160件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量每天就相应减少20件,设这种商品的销售单价为x元,商场每天销售这种商品y件(1)给定x的一些值,请计算y的值,填在表中
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … | 160 | 140 | 120 | 100 | 80 | … |
(3)当商品的销售单价定为多少元时,该商品销售这种商品能获得的利润为420元?这时每天销售的商品是多少件?
分析 (1)根据销售单价每提高1元,销售量每天就相应减少20件,计算即可;
(2)由销售单价为x元得到销售减少量20(x-7),用160减去销售减少量得到y与x的函数关系式;
(3)根据“利润值=(销售单价-购进单价)×{160-20(销售单价-7)}”,列出一元二次方程.
解答 解:(1)x=8,y=160-20=140;x=11,y=160-20(11-7)=80;
故填140,80.
(2)y=160-20(x-7)=-20x+300;
(3)根据题意列方程,420=(x-5)[160-20(x-7)]
整理得:-20x2+400x-1920=0
解得:x1=8,x2=12,
当x=8时,y=140;当x=12时,y=60;
所以当商品的销售单价定为8元或12元时,该商品销售这种商品能获得的利润为420元;商品的销售单价定为8元时,每天销售商品140件;商品的销售单价定为12元时,每天销售商品60件.
点评 本题考查了函数模型以及一元二次方程应用,数学建模思想方法,正确理解题意列出代数式是解决问题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
9.分式方程$\frac{2x}{x-1}$=3的解为( )
| A. | x=4 | B. | x=3 | C. | x=2 | D. | x=-1 |
7.若方程组$\left\{\begin{array}{l}{x+y=1}\\{2x+ay=b}\end{array}\right.$有唯一解,那么a,b的值应当是( )
| A. | a≠2,b为任意实数 | B. | a=2,b≠0 | C. | a=2,b≠2 | D. | a,b为任意实数 |
9.已知平行四边形的一边为2,则下列数据中,能分别作为它的两条对角线长的是( )
| A. | 8,6 | B. | 10,12 | C. | 20,6 | D. | 12,12 |
 如图,在△ABC中,AC⊥BC,CE⊥AB于E,AF平分∠CAB交CE于点F,过点F作FD∥BC交AB于点D,说明AC=AD成立的理由.
如图,在△ABC中,AC⊥BC,CE⊥AB于E,AF平分∠CAB交CE于点F,过点F作FD∥BC交AB于点D,说明AC=AD成立的理由.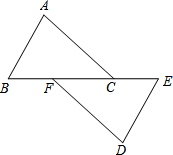 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,试说明AC与DF平行的理由.
如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=EC,试说明AC与DF平行的理由.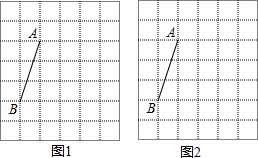 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.