题目内容
3.已知关于x的方程$\frac{1}{4}$x2-(m-2)x+m2=0有两个相等的实数根,则方程的根为( )| A. | x1=x2=1 | B. | x1=x2=-2 | C. | x1=x2=-1 | D. | x1=x2=2 |
分析 由一元二次方程$\frac{1}{4}$x2+(m-2)x+m2=0有两个相等的实数根,得△=0,即△=(m-2)2-m2=-4m+4=0,可解得m=1,然后把m=1代入方程得$\frac{1}{4}$x2+(m-2)x+m2=0,解此方程即可.
解答 解:∵关于x的一元二次方程$\frac{1}{4}$x2-(m-2)x+m2=0有两个相等的实数根,
∴△=0,即△=(m-2)2-m2=-4m+4=0,
解方程-4m+4=0,得m=1.
所以原方程变为:$\frac{1}{4}$x2+x+1=0,($\frac{1}{2}$x+1)2=0,则x1=x2=-2.
故选B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
13.某校运动员分组训练,若每组6人,余3人;若每组7人,则缺5人;设运动员人数为x 人,组数为y组,则列方程组为( )
| A. | $\left\{\begin{array}{l}{6y=x+3}\\{7y=x+5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6y=x-3}\\{7y+5=x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{6y=x+3}\\{7y+5=x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6y=x-3}\\{7y=x+5}\end{array}\right.$ |
 如图,在△ABC中,AC⊥BC,CE⊥AB于E,AF平分∠CAB交CE于点F,过点F作FD∥BC交AB于点D,说明AC=AD成立的理由.
如图,在△ABC中,AC⊥BC,CE⊥AB于E,AF平分∠CAB交CE于点F,过点F作FD∥BC交AB于点D,说明AC=AD成立的理由.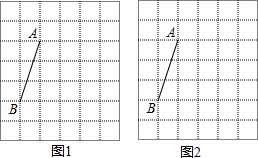 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
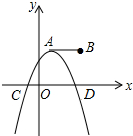 如图,点A,B的坐标分别为(1,3)和(5,3),抛物线y=a(x-h)2+k的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为9.
如图,点A,B的坐标分别为(1,3)和(5,3),抛物线y=a(x-h)2+k的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为9. 如图,直线y=mx+n与双曲线y=$\frac{k}{x}$相交于A(-1,2),B(2,b)两点,与y轴相交于点C.
如图,直线y=mx+n与双曲线y=$\frac{k}{x}$相交于A(-1,2),B(2,b)两点,与y轴相交于点C.