题目内容
4. 在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.(1)求出图中格点四边形DEFG对应的S=3,N=1,L=6.
(2)已知格点多边形的面积可表示为S=N+aL+b,其中a,b为常数,
①求a,b的值;
②若某格点多边形对应的N=82,L=38,求S的值.
分析 (1)直接观察图形即可得出结论;
(2)①先根据图形得出图中格点三角形ABC的面积为1,格点四边形DEFG的面积为3,进而代入格点多边形的面积公式即可求出a,b;
②代入①中得出的格点多边形的面积公式即可得出结论.
解答 解:(1)观察图形,可得S=3,N=1,L=6;
故答案为:3,1,6;
(2)由图知,图中格点三角形ABC的面积为1,格点四边形DEFG的面积为3,
∵格点多边形的面积S=N+aL+b,
∴结合图中的格点三角形ABC及格点四边形DEFG可得,$\left\{\begin{array}{l}{4a+b=1}\\{1+6a+b=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-1}\end{array}\right.$,
(3)由(2)知,a=$\frac{1}{2}$,b=-1,∴S=N+$\frac{1}{2}$L-1,
将N=82,L=38代入S=N+$\frac{1}{2}$L-1,得S=82+$\frac{1}{2}$×38-1=100.
故答案为:3,1,6;
点评 本题考查新定义的理解,也考查了学生分析、解决问题的能力,注意区分多边形内部格点数和边界格点数是解本题的关键.

练习册系列答案
相关题目
14.下列各式是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{{x}^{2}+1}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{\frac{5}{3}}$ |
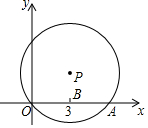 如图所示,在平面直角坐标系中,点P在第一象限,⊙P与x轴交于O、A两点,点B是OA的中点,点B的坐标为(3,0),⊙P的半径为$\sqrt{13}$,则点P的坐标为(3,2).
如图所示,在平面直角坐标系中,点P在第一象限,⊙P与x轴交于O、A两点,点B是OA的中点,点B的坐标为(3,0),⊙P的半径为$\sqrt{13}$,则点P的坐标为(3,2).