Question

13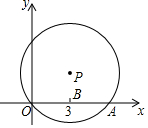．如图所示，在平面直角坐标系中，点P在第一象限，⊙P与x轴交于O、A两点，点B是OA的中点，点B的坐标为（3，0），⊙P的半径为$\sqrt{13}$，则点P的坐标为（3，2）．

Answer 1

分析 连接OB、OP，根据垂径定理可得PB⊥OA，在直角△OPB中利用三角函数求得PB的值，则P的坐标即可求得．

解答 解：连接OB、OP．
∵B是OA的中点，
∴PB⊥OA．
在直角△OPB中，PB=$\sqrt{O{P}^{2}-O{B}^{2}}$=$\sqrt{13-9}$=2，
则P的坐标是（3，2）．

点评 本题考查了垂径定理，以及坐标与图形的性质，求点的坐标的问题就是求线段的长度的问题．