题目内容
 如图,A、B两个小集镇在河流l的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水.
如图,A、B两个小集镇在河流l的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水.(1)请你在河流l上选择水厂的位置M,使铺设水管的费用最节省?
(2)若铺设水管的费用为每千米3万元,请你求出(1)中铺设水管的费用是多少?
考点:轴对称-最短路线问题
专题:
分析:先作点A的对称点A′,连接点B和点A′,交l于点M,M即所求作的点,过点A′作AA′的垂线,延长BD交AA′于点K,根据轴对称的性质,知:MA+MB=A′B.根据勾股定理即可求解.
解答:解:(1)作A关于直线l的对称点A′,连接A′B交l于点M,点M即为所求.
如图所示:
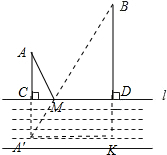
(2)过点A′作A′K⊥BD,交BD的延长线于点K.
∵AC∥BD,CD∥A′K,
∴A′K=CD=60千米,BK=BD+DK=60+20=80千米,
在Rt△A′BK中,
A′B=
=
=50(千米).
∴AM+MB=50.
即铺设水管的最短长度为50千米,
∵铺设水管的费用为每千米3万元,
∴所需费用=50×3=150(万元).
答:铺设水管的费用是150万元.
如图所示:

(2)过点A′作A′K⊥BD,交BD的延长线于点K.
∵AC∥BD,CD∥A′K,
∴A′K=CD=60千米,BK=BD+DK=60+20=80千米,
在Rt△A′BK中,
A′B=
| A′K2+BK2 |
| 302+402 |
∴AM+MB=50.
即铺设水管的最短长度为50千米,
∵铺设水管的费用为每千米3万元,
∴所需费用=50×3=150(万元).
答:铺设水管的费用是150万元.
点评:本题考查的是轴对称-最短路线问题,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
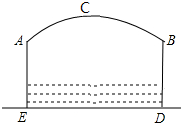 如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m.试以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系,求题中抛物线的函数表达式.
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m.试以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系,求题中抛物线的函数表达式.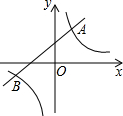 如图,直线y=kx+b与双曲线y=
如图,直线y=kx+b与双曲线y= 如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=140°,∠E=80°,试求∠F的度数.
如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=140°,∠E=80°,试求∠F的度数.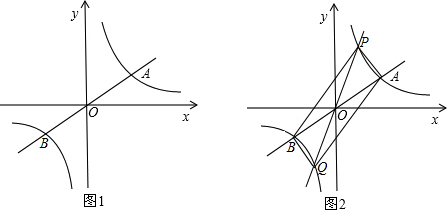
 如图,在所给网格中每小格均为边长是1的正方形,△ABC的顶点均在格点上,请完成下列各题:(用直尺画图)
如图,在所给网格中每小格均为边长是1的正方形,△ABC的顶点均在格点上,请完成下列各题:(用直尺画图)