题目内容
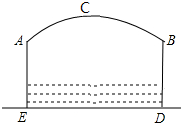 如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m.试以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系,求题中抛物线的函数表达式.
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m.试以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系,求题中抛物线的函数表达式.考点:二次函数的应用
专题:
分析:首先建立平面直角坐标系,进而利用顶点式求出函数解析式,即可得出答案.
解答: 解:如图所示.
解:如图所示.
由题知抛物线的顶点坐标为(0,11),B(8,8),
设抛物线的表达式为y=ax2+11,
将点B的坐标(8,8)代入抛物线的表达式得:a=-
,
所以抛物线的表达式为:y=-
x2+11.
 解:如图所示.
解:如图所示.由题知抛物线的顶点坐标为(0,11),B(8,8),
设抛物线的表达式为y=ax2+11,
将点B的坐标(8,8)代入抛物线的表达式得:a=-
| 3 |
| 64 |
所以抛物线的表达式为:y=-
| 3 |
| 64 |
点评:此题主要考查了二次函数的应用,正确建立平面直角坐标系是解题关键.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
有A,B两只不透明口袋,每只口袋里装有两只相同的球,A袋中的两只球上分别写了“细”、“心”的字样,B袋中的两只球上分别写了“信”、“任”的字样,从每只口袋里各摸出一只球,能组成“信心”字样的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接六边形的面积为( )
如图所示,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接六边形的面积为( )A、
| ||||
B、6
| ||||
| C、8 | ||||
| D、16 |
下列比较一对数的大小时,正确的是( )
A、-
| ||||
| B、-1.5>-1.4 | ||||
| C、-896>0.01 | ||||
| D、-(+5.5)>-|-4.5| |
等腰三角形的两边长分别为3cm和7cm,则周长为( )cm.
| A、13 | B、17 |
| C、13或17 | D、17或11 |
 如图,A、B两个小集镇在河流l的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水.
如图,A、B两个小集镇在河流l的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水.