题目内容
10.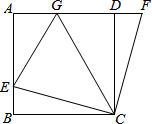 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;
(2)△CDF可看成图中哪个三角形通过旋转变换得到的?写出旋转过程;
(3)若点G在AD上,且∠GCE=45°,试判断线段GE,BE,GD之间的数量关系,并说明理由.
分析 (1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF;
(2)△CDF可以看成是△CBE绕点C顺时针旋转90°得到的;
(3)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.
解答 (1)证明:在正方形ABCD中,
∵BC=CD,∠B=∠CDF,BE=DF,
在△CBE与△CDF中,$\left\{\begin{array}{l}{BC=CD}\\{∠B=∠CDF}\\{BE=DF}\end{array}\right.$,
∴△CBE≌△CDF(SAS),
∴CE=CF;
(2)解:△CDF可以看成是△CBE绕点C顺时针旋转90°得到的;
(3)解:GE=BE+GD,理由:
由(1)得△CBE≌△CDF,
∴∠BCE=∠DCF,CE=CF.
∵∠GCE=45°,
∴∠BCE+DCG=45°,
∴∠GCF=∠DCF+∠DCG=45°,
在△ECG与△FCG中,
$\left\{\begin{array}{l}{CE=CF}\\{∠GCE=∠GCF}\\{GC=GC}\end{array}\right.$,
∴△ECG≌△FCG(SAS),
∴GE=GF,
∴GE=DF+GD=BE+GD.
点评 本题主要考查图形的旋转,证两条线段相等往往转化为证明这两条线段所在三角形全等的思想,在第二问中也是考查了通过全等找出和GE相等的线段,从而得出线段GE,BE,GD之间的数量关系.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
18.分解因式m-ma2的结果是( )
| A. | m(1+a)(1-a) | B. | m(1+a)2 | C. | mm(1-a)2 | D. | (1-a)(1+a) |
5.关于x的一元二次方程x2-3x+m=0有两个不相等的实数根,则实数m的取值范围为( )
| A. | m≥$\frac{9}{4}$ | B. | m<$\frac{9}{4}$ | C. | m=$\frac{9}{4}$ | D. | m<-$\frac{9}{4}$ |
15.直角三角形两条直角边长为3cm和4cm,斜边上的高为( )
| A. | 3cm | B. | 2.4cm | C. | 2cm | D. | 3.6cm |
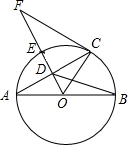 如图,AB是⊙O的直径,OD垂直弦AC于点D,OD的延长线交⊙O 于点E,与过点C的⊙O的切线交于点F,已知OD=3,DE=2.
如图,AB是⊙O的直径,OD垂直弦AC于点D,OD的延长线交⊙O 于点E,与过点C的⊙O的切线交于点F,已知OD=3,DE=2. 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.
如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.