题目内容
20.已知$\frac{3x+2z}{4}=\frac{3y+z}{5}=\frac{5x+y-z}{6}=2$.求x,y,z的值.分析 已知等式整理为三元一次方程组,求出方程组的解即可得到x,y,z的值.
解答 解:已知等式整理得:$\left\{\begin{array}{l}{3x+2z=8①}\\{3y+z=10②}\\{5x+y-z=12③}\end{array}\right.$,
①+③×2得:13x+2y=32④,
②+③得:5x+4y=22⑤,
④×2-⑤得:21x=42,即x=2,
把x=2代入④得:y=3,
把y=3代入②得:z=1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\\{z=1}\end{array}\right.$.
点评 此题考查了解三元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.下列调查方式合适的是( )
| A. | 对载人航天器“嫦娥二号”零部件的检查,采用抽样调查的方式 | |
| B. | 了解炮弹的杀伤力,采用全面调查的方式 | |
| C. | 对电视剧《来自星星的你》收视率的调查,采用全面调查的方式 | |
| D. | 对建阳市食品合格情况的调查,采用抽样调查的方式 |
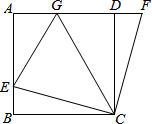 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.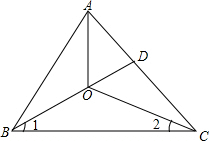 如图所示,在△ABC中,∠ABC、∠ACB的平分线交于O,BO的延长线交AC于D,连接AO,且∠1=30°,∠2=20°,求∠AOD的度数.
如图所示,在△ABC中,∠ABC、∠ACB的平分线交于O,BO的延长线交AC于D,连接AO,且∠1=30°,∠2=20°,求∠AOD的度数. 如图,点A、B、C在⊙O上,且四边形OABC是一平行四边形.
如图,点A、B、C在⊙O上,且四边形OABC是一平行四边形.