题目内容
9.阅读下列材料:正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.
数学老师给小明同学出了一道题目:在图1正方形网格(每个小正方形边长为1)中画出格点△ABC,使AB=AC=$\sqrt{5}$,BC=$\sqrt{2}$;
小明同学的做法是:由勾股定理,得AB=AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,于是画出线段AB、AC、BC,从而画出格点△ABC.
(1)请你参考小明同学的做法,在图2正方形网格(每个小正方形边长为1)中画出格点△A′B′C′(A′点位置如图所示),使AB′=A′C′=5,B′C′=$\sqrt{10}$.(直接画出图形,不写过程);
(2)观察△ABC与△A′B′C′的形状,猜想∠BAC与∠B′A′C′有怎样的数量关系,并证明你的猜想.

分析 (1)根据勾股定理,作B'C'=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,A'B'=$\sqrt{{3}^{2}+{4}^{2}}$=5,画出图形即可;
(2)根据相似三角形的判定定理,得出△ABC∽△A′B′C′,由相似三角形的性质即可得出结论.
解答 解:(1)如图所示,△A′B′C′即为所求;
(2)猜想:∠BAC=∠B′A′C′.
证明:∵$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{\sqrt{5}}{5}$,
$\frac{BC}{B′C′}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$,
∴$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$,
∴△ABC∽△A′B′C′,
∴∠BAC=∠B′A′C′.
点评 本题考查的是勾股定理的应用以及相似三角形的判定与性质,解题时注意:在任何一个直角三角形中,两条直角边长的平方之和等于斜边长的平方,这是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( )
如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( )
 如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( )
如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( )| A. | 变长了1.5米 | B. | 变短了2.5米 | C. | 变长了3.5米 | D. | 变短了3.5米 |
 如图,在四边形ABCD中,AD∥BC,∠ABC=∠DCB,点E、F分别在AB、DC上,且BE=2EA,CF=2FD.试证明:∠BEC=∠CFB.
如图,在四边形ABCD中,AD∥BC,∠ABC=∠DCB,点E、F分别在AB、DC上,且BE=2EA,CF=2FD.试证明:∠BEC=∠CFB.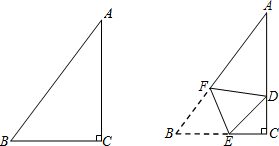
 如图所示,在△ABC中,D是BC上的一点,连接AD,若AC2=CD•BC,则图中有1对相似三角形,分别是△ADC∽△BAC.
如图所示,在△ABC中,D是BC上的一点,连接AD,若AC2=CD•BC,则图中有1对相似三角形,分别是△ADC∽△BAC.