Question

14．如图，三角形纸片ABC中，∠C=90°，AC=4，BC=3．将纸片折叠，使点B落在AC边上的点D处，折痕与BC，AB分别交于点E，F．
（1）设BE=x，DC=y，求y关于x的函数关系式，并确定自变量x的取值范围；
（2）当△ADF是直角三角形时，求BE的长．

Answer 1

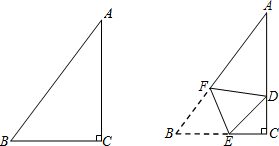
分析 （1）根据勾股定理即可得出y²+（3-x）²=x²，从而得出y=$\sqrt{6x-9}$，由于当E和C重合时，x最大，最大值为3，6x-9≥0，即可求得x的取值；
（2）分两种情况分别讨论即可求得．

解答 解：（1）∵BE=x，
∴DE=x，EC=3-x，
在RT△DEC中，DC²+EC²=DE²，即y²+（3-x）²=x²，
∴y=$\sqrt{6x-9}$，
当E和C重合时，x最大，最大值为3，
∴$\frac{3}{2}$≤x≤3；

（2）分两种情况：
①如图1，当∠ADF=90°时，则FD∥BC，
∴∠AFD=∠B，
∵∠EDF=∠B，
∴∠AFD=∠EDF，
∴DE∥AB，
∴△DEC∽△ABC，
∴$\frac{DE}{AB}=\frac{CE}{BC}$，即$5\frac{x}{\;}$=$\frac{3-x}{3}$，
解得x=$\frac{15}{8}$，
∴BE=$\frac{15}{8}$
②如图2，当∠AFD=90°时，作EH⊥AB于H，则△BEH∽△BAC，
∵BE=x，
∴BH=$\frac{3}{5}$x，HE=$\frac{4}{5}$x，
∵∠BFE=45°，
∴HF=HE=$\frac{4}{5}$x，
∴BF=DF=$\frac{7}{5}$x，
∴AF=5-$\frac{7}{5}$x，
∵△ADF∽△ABC，
∴$\frac{\frac{7}{5}x}{5-\frac{7}{5}x}$=$\frac{3}{4}$，
解得x=$\frac{75}{49}$，即BE=$\frac{75}{49}$，
∴由①②得，BE=$\frac{15}{8}$或$\frac{75}{49}$．

点评 该题主要考查了翻折变换的性质及其应用问题；解题的关键是灵活运用勾股定理等几何知识点来分析、判断、推理或解答；对综合的分析问题解决问题的能力提出了较高的要求．