题目内容
两个同心圆中大圆的弦AB与小圆相切于点C，AB=8，则形成的圆环的面积为（ ）
| A、无法求出 | B、8 |
| C、8π | D、16π |
考点：切线的性质,勾股定理,垂径定理
专题：计算题
分析：画出图形，如图所示，由小圆与AB相切，利用切线的性质得到OC垂直于AB，利用垂径定理得到C为AB中点，求出AC的长，在直角三角形AOC中，利用勾股定理求出OA2-OC2的值，由大圆面积减去小圆面积求出圆环面积即可．
解答：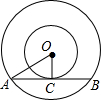
解：如图所示，
∵弦AB与小圆相切，
∴OC⊥AB，
∴C为AB的中点，
∴AC=BC=
AB=4，
在Rt△AOC中，根据勾股定理得：OA2-OC2=AC2=16，
则形成圆环的面积为πOA2-πOC2=π（OA2-OC2）=16π，
故选D．
解：如图所示，∵弦AB与小圆相切，
∴OC⊥AB，
∴C为AB的中点，
∴AC=BC=
| 1 |
| 2 |
在Rt△AOC中，根据勾股定理得：OA2-OC2=AC2=16，
则形成圆环的面积为πOA2-πOC2=π（OA2-OC2）=16π，
故选D．
点评：此题考查了切线的性质，勾股定理，以及垂径定理，熟练掌握切线的性质是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在小正方形的边长都为1的方格纸中，△ABO的顶点都在小正方形的顶点上．
如图，已知EO⊥AB于点O，OE平分∠MON，那么∠1与∠2相等吗？为什么？
如图所示，抛物线y=-x2+mx+n经过点A（1，0）和点C（4，0），与y轴交于点B．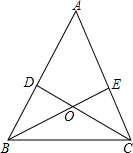
如图，△ABC中，BE，CD为角平分线且交点为点O，当∠A=60°时，
在△ABC中，BO、CO分别平分∠CBA、∠BCA，求证：∠COB=
如图，在Rt△ABC中，∠B=90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知∠BAE=16°，求∠C的度数？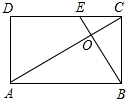
E是矩形ABCD的边CD上的点，BE交AC于点O，已知△COE与△AOB的面积分别为2和32，则四边形AOED的面积为
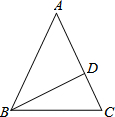在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠CAB=