题目内容
 如图所示,抛物线y=-x2+mx+n经过点A(1,0)和点C(4,0),与y轴交于点B.
如图所示,抛物线y=-x2+mx+n经过点A(1,0)和点C(4,0),与y轴交于点B.(1)求抛物线所对应的解析式.
(2)连接直线BC,抛物线的对称轴与BC交于点E,F为抛物线的顶点,求四边形AECF的面积.
考点:待定系数法求二次函数解析式,二次函数的性质
专题:计算题
分析:(1)利用交点式可直接写出抛物线的解析式;
(2)先把解析式配成顶点式得到F的坐标(
,
),在确定B点坐标,接着利用待定系数法求出直线BC的解析式,则可确定E点坐标,然后利用四边形AECF的面积=S△ACE+S△ACF进行计算.
(2)先把解析式配成顶点式得到F的坐标(
| 5 |
| 2 |
| 9 |
| 4 |
解答:解:(1)抛物线解析式为y=-(x-1)(x-4)=-x2+5x-4;
(2)y=-x2+5x-4=-(x-
)2+
,则抛物线的对称轴为直线x=
,顶点F的坐标为(
,
);
当x=0时,y=-x2+5x-4=-4,则B点坐标为(0,-4)
设直线BC的解析式为y=kx+b,
把B(0,-4),C(4,0)代入得
,解得
,
则直线BC的解析式为y=x-4,
当x=
时,y=x-4=
-4=-
,则E点坐标为(-
,0),
所以四边形AECF的面积=S△ACE+S△ACF
=
×(4-1)×
+
×(4-1)×
=
.
(2)y=-x2+5x-4=-(x-
| 5 |
| 2 |
| 9 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 9 |
| 4 |
当x=0时,y=-x2+5x-4=-4,则B点坐标为(0,-4)
设直线BC的解析式为y=kx+b,
把B(0,-4),C(4,0)代入得
|
|
则直线BC的解析式为y=x-4,
当x=
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
所以四边形AECF的面积=S△ACE+S△ACF
=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
=
| 45 |
| 8 |
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
三条互不重合的直线的交点个数可能是( )
| A、0,1,3 |
| B、0,2,3 |
| C、0,1,2,3 |
| D、0,1,2 |
估算
值是( )
| 34 |
| A、在2和3之间 |
| B、在3和4之间 |
| C、在4和5之间 |
| D、在5和6之间 |
两个同心圆中大圆的弦AB与小圆相切于点C,AB=8,则形成的圆环的面积为( )
| A、无法求出 | B、8 |
| C、8π | D、16π |
 如图,射线OC、OD、OE是∠AOB四等分线,图中所有的角的度数之和为360°,则∠AOB的度数等于
如图,射线OC、OD、OE是∠AOB四等分线,图中所有的角的度数之和为360°,则∠AOB的度数等于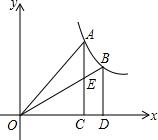 如图,过反比例函数y=
如图,过反比例函数y=