题目内容
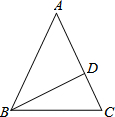 在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠CAB=
在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠CAB=考点:等腰三角形的性质
专题:
分析:由BD=BC=AD可知,△ABD,△BCD为等腰三角形,设∠A=∠ABD=x,则∠C=∠CDB=2x,又由AB=AC可知,△ABC为等腰三角形,则∠ABC=∠C=2x,在△ABC中,用内角和定理列方程求解.
解答:解:∵BD=BC=AD,
∴△ABD,△BCD为等腰三角形,
设∠A=∠ABD=x,则∠C=∠CDB=2x,
又∵AB=AC可知,
∴△ABC为等腰三角形,
∴∠ABC=∠C=2x,
在△ABC中,∠A+∠ABC+∠C=180°,
即x+2x+2x=180°,
解得x=36°,
即∠CAB=36°,
∴∠CDB=72°.
故本题答案为:36°,72°.
∴△ABD,△BCD为等腰三角形,
设∠A=∠ABD=x,则∠C=∠CDB=2x,
又∵AB=AC可知,
∴△ABC为等腰三角形,
∴∠ABC=∠C=2x,
在△ABC中,∠A+∠ABC+∠C=180°,
即x+2x+2x=180°,
解得x=36°,
即∠CAB=36°,
∴∠CDB=72°.
故本题答案为:36°,72°.
点评:本题考查了等腰三角形的性质.关键是利用等腰三角形的底角相等,外角的性质,内角和定理,列方程求解.

练习册系列答案
相关题目
两个同心圆中大圆的弦AB与小圆相切于点C,AB=8,则形成的圆环的面积为( )
| A、无法求出 | B、8 |
| C、8π | D、16π |
已知下列命题:①两条直线被第三条直线所截,如果同位角相等,那么两直线平行;②相等的角是对顶角;③同角的余角相等;④三角形的一个外角等于和它不相邻的两个内角和.其中真命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
若关于x的一元二次方程的两个根为x1=1,x2=2,则这个方程是( )
| A、x2+3x-2=0 |
| B、x2-3x+2=0 |
| C、x2-3x+3=0 |
| D、x2+3x+2=0 |