题目内容
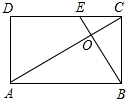E是矩形ABCD的边CD上的点，BE交AC于点O，已知△COE与△AOB的面积分别为2和32，则四边形AOED的面积为考点：矩形的性质
专题：
分析：由矩形的性质易证△COE∽△AOB，所以可求出OE：OB的值，再根据等高的两三角形的面积之比等于底之比可求出△BOC，进而可以求出△ABC的面积，即△ADC的面积，从而求出四边形AOED的面积．
解答：解：∵四边形ABCD是矩形，
∴AB∥CD，
∴△COE∽△AOB，
∵△COE与△AOB的面积分别为2和32，
∴OE：OB=1：4，
∴S△BOC=8，
∴S△ABC=8+32=40，
∴S△ADC=S△ABC=8+32=40，
∴四边形AOED的面积=40-2=38，
故答案为：38．
∴AB∥CD，
∴△COE∽△AOB，
∵△COE与△AOB的面积分别为2和32，
∴OE：OB=1：4，
∴S△BOC=8，
∴S△ABC=8+32=40，
∴S△ADC=S△ABC=8+32=40，
∴四边形AOED的面积=40-2=38，
故答案为：38．
点评：本题考查了矩形的性质的运用，等高的两三角形的面积的运用，相似三角形的判定及性质的运用，解答时由等高的两三角形的面积关系入手是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，射线OC、OD、OE是∠AOB四等分线，图中所有的角的度数之和为360°，则∠AOB的度数等于两个同心圆中大圆的弦AB与小圆相切于点C，AB=8，则形成的圆环的面积为（ ）
| A、无法求出 | B、8 |
| C、8π | D、16π |