Question

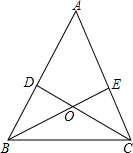如图，△ABC中，BE，CD为角平分线且交点为点O，当∠A=60°时，
（1）求∠BOC的度数；
（2）当∠A=100°时，求∠BOC的度数；
（3）若∠A=α°时，求∠BOC的度数．

Answer 1

考点：三角形内角和定理

专题：

分析：（1）在△ABC中利用三角形内角和定理和角平分线的定义可求得∠OBC+∠OCB，在△BOC中利用三角形内角和定理可求得∠BOC；（2）方法同（1）；（3）方法同（1）．

解答：解：
∵BE，CD为角平分线，
∴∠OBC=

1

2

∠ABC，∠OCB=

1

2

∠ACB，
∵∠A+∠ABC+∠ACB=180°，
∴∠ABC+∠ACB=180°-∠A，
∴

1

2

∠ABC+

1

2

∠ACB=

1

2

（180°-∠A）=90°-

1

2

∠A，
∴∠OBC+∠OCB=90°-

1

2

∠A，
又∠BOC+∠OBC+∠OCB=180°，
∴∠BOC=180°-（∠OBC+∠OCB）=180°-（90°-

1

2

∠A）=90°+

1

2

∠A，
（1）当∠A=60°时，∠BOC=90°+

1

2

×60°=120°；
（2）当∠A=100°时，∠BOC=90°+

1

2

×100°=140°；
（3）当∠A=α°时，∠BOC=90°+

1

2

α°．

点评：本题主要考查三角形内角和定理及角平分线的定义，掌握三角形内角和为180°是解题的关键．