题目内容
5．一个杂技演员荡秋千，秋千绳子的长度为3.2米，当秋千向两边摆动的摆角恰好为60°时（摆动时两边的最高点与地面的距离相同），求摆动过程中最高点与最低点的高度差（精确到0.1米）．分析 根据题意可以画出相应的图形，从而可以求得摆动过程中最高点与最低点的高度差．
解答 
解：如右图所示，
∵OA=OB=OD=3.2米，∠BOD=60°，
∴∠BOC=30°，
∵OA⊥BD于点C，
∴OC=OB•cos30°，
∴CA=OA-OC=3.2-3.2×cos30°≈0.4（米），
即摆动过程中最高点与最低点的高度差0.4米．
点评 本题考查解直角三角形的应用，解题的关键是明确题意，找出所求问题需要的条件．
练习册系列答案
相关题目
16．秋季运动会即将召开，渝北校区将对校园进行彩旗装扮，计划把主干道一侧全部插上彩旗，要求路的两端各插一面，并且每两面旗帜的间隔相等．如果每隔4米插一面，则彩旗差23面；如果每隔5米插1面，则彩旗正好用完．设原有彩旗x面，主干道长为y米，则根据题意列出方程组正确的是（ ）
| A． | $\left\{\begin{array}{l}{\frac{y}{4}=x+23}\\{\frac{y}{5}+1=x}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{\frac{y}{4}+1=x+23}\\{\frac{y}{5}+1=x}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{\frac{y}{4}+1=x+23}\\{\frac{y}{5}=x}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{\frac{y}{4}=x+23}\\{\frac{y}{5}=x}\end{array}\right.$ |
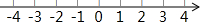在数轴上画出表示下列各数的点，并回答下列问题：
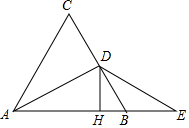如图，在等边三角形ABC中，D是BC边的中点，E是AB延长线上的一点，且BE=BD，过点D作DH⊥AB于H．