题目内容
14.现在有4个小长方体纸盒,每个的长、宽、高都分别是a,b,c,a>2b且b>2c,若用这4个长方体纸盒搭成一个大长方体,共有6种不同的方式,搭成的大长方体的表面积最小为4(ab+ac+2bc)cm2,(用含a,b,c的代数式表示)分析 分四个小长方体排一行以及两行来寻找搭法,由此可得出共6种不同的搭建方式,再根据长方体的表面积公式结合a>2b、b>2c即可得出大长方体的表面积最小值.
解答 解:四个小长方体排一行时,有3种不同的搭法;四个小长方体排两行时,有3种不同的搭法.
∴用这4个长方体纸盒搭成一个大长方体,共有6种不同的方法.
∵a>2b且b>2c,
∴搭成的大长方体的表面积最小为:4×2×(ab+ac+bc)-4×(ab+ac)=4(ab+ac+2bc)cm2.
故答案为:6;4(ab+ac+2bc).
点评 本题考查了几何体的表面积,分两类搭建方式寻找搭法是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
4.某钢铁厂6月份的产量是50吨,比5月份增长x%,那么今年5月份这种钢的产量是( )
| A. | 50(1+x%) | B. | $\frac{50}{1+x%}$ | C. | 50(1-x%) | D. | $\frac{50}{1-x%}$ |
 在△ABC中,DE∥BC,AC=4,AB=3,EC=1,求AD和BD.
在△ABC中,DE∥BC,AC=4,AB=3,EC=1,求AD和BD.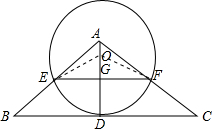 如图,在△ABC中,D为边BC的中点,O是AD上一点,⊙O与BC相切于点D,且与AB、AC分别相交于点E、F,连接EF交AD于点G.
如图,在△ABC中,D为边BC的中点,O是AD上一点,⊙O与BC相切于点D,且与AB、AC分别相交于点E、F,连接EF交AD于点G.