题目内容
15.△ABC内接于⊙O,AB=4,AC=6.(1)如图1,AD平分∠BAC交⊙O于D,DE⊥AC于E,求CE长;
(2)如图2,AD平分△ABC外角∠MAC交⊙O于D,DE⊥AC于E,直接写出CE的长为5.
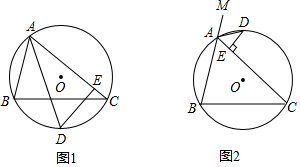
分析 (1)如图1,作辅助线,构建全等三角形,利用HL证明Rt△DBF≌Rt△DCE,得CE=BF,设CE=x,再证明Rt△AFD≌Rt△AED,得AE=AF,并根据AE=AF列一元一次方程,求出x的值,即是CE的值;
(2)如图2,作辅助线,构建全等三角形,同理证明Rt△DBF≌Rt△DCE,CE=BF,又得AE=AF,设AE=x,列方程为4+x=6-x,x=1,则CE=5.
解答  解:(1)如图1,过D作DF⊥AB,交AB的延长线于F,连接BD、CD,
解:(1)如图1,过D作DF⊥AB,交AB的延长线于F,连接BD、CD,
∵AD平分∠BAC,DE⊥AC,
∴DF=DE,∠BAD=∠DAC,
∵∠BAD=∠BCD,∠DAC=∠DBC,
∴∠DBC=∠BCD,
∴BD=CD,
在Rt△DBF和Rt△DCE中,
∵$\left\{\begin{array}{l}{BD=CD}\\{DF=DE}\end{array}\right.$,
∴Rt△DBF≌Rt△DCE(HL),
∴CE=BF,
设CE=x,则AE=6-x,BF=x,AF=4+x,
在Rt△AFD和Rt△AED中,
∵$\left\{\begin{array}{l}{AD=AD}\\{DF=DE}\end{array}\right.$,
∴Rt△AFD≌Rt△AED(HL),
∴AF=AE,
则4+x=6-x,
x=1,
∴CE=1;
(2)如图2,过D作DF⊥BM于F,连接DB、DC,
∵AD平分∠MAC,DE⊥AC,
∴DF=DE,∠MAD=∠DAC,
∵∠MAD=∠BCD,∠DAC=∠DBC,
∴∠DBC=∠BCD,
∴BD=CD,
在Rt△DBF和Rt△DCE中,
∵$\left\{\begin{array}{l}{BD=CD}\\{DF=DE}\end{array}\right.$,
∴Rt△DBF≌Rt△DCE(HL),
∴CE=BF,
同理得:AE=AF,
设AE=x,则AF=x,
则4+x=6-x,
x=1,
∴CE=AC-AE=6-1=5.
故答案为:5.
点评 本题考查了三角形的外接圆、角平分线的性质和圆周角定理,恰当地作辅助线构建三角形全等是本题的关键;熟练掌握角平分线的性质到角两边的距离相等,利用同弧所对的圆周角相等及圆内接四边形的一个外角等于其内对角,证明角相等,从而得出边相等,为全等创造条件,并与方程相结合得出结论.

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
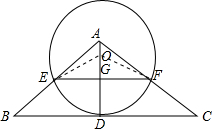 如图,在△ABC中,D为边BC的中点,O是AD上一点,⊙O与BC相切于点D,且与AB、AC分别相交于点E、F,连接EF交AD于点G.
如图,在△ABC中,D为边BC的中点,O是AD上一点,⊙O与BC相切于点D,且与AB、AC分别相交于点E、F,连接EF交AD于点G.